I. Проекции и преобразования.
На первом занятии вы познакомились с простейшим проектором для театра теней. Для него нужен источник света (лампа, фонарик, светодиод, солнце) и экран (лист бумаги, стена, поверхность пола и прочие поверхности). В предыдущих домашних работах вы пробовали его делать. Вы уже знаете, что если лучи света параллельны друг другу, то такая проекция называется параллельной, а если нет- то перспективной. Последняя так называется, потому что в проекции будет точка схода, где проекции параллельных линий сходятся . Вот такая любопытная особенность. В перспективной проекции лучи света исходят из одной точки (Рис.1).
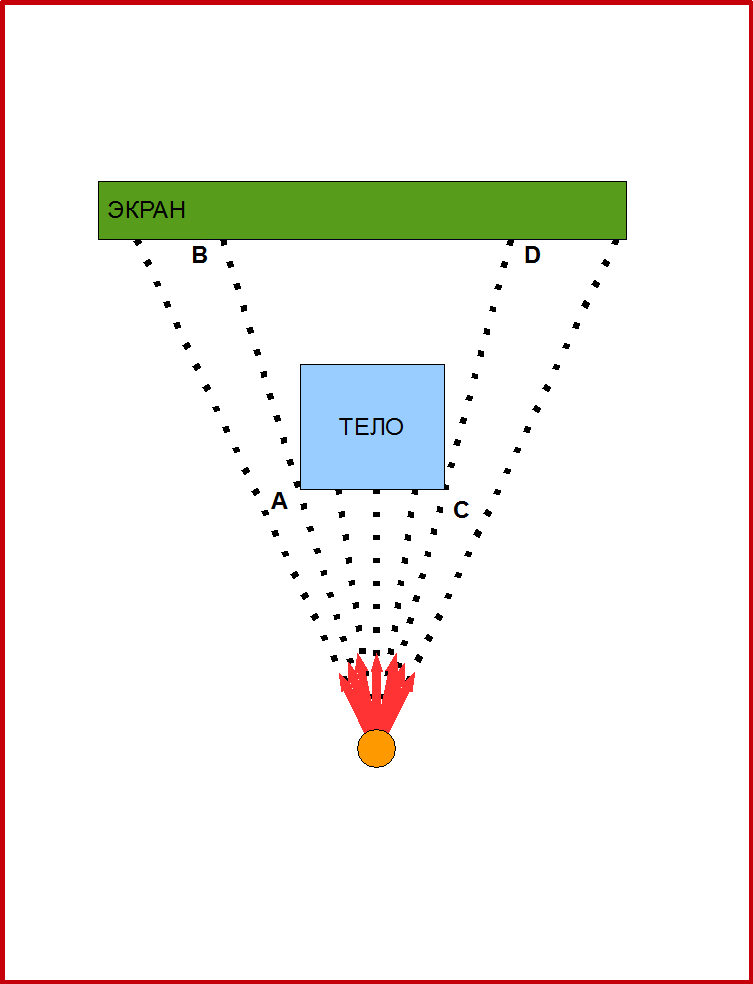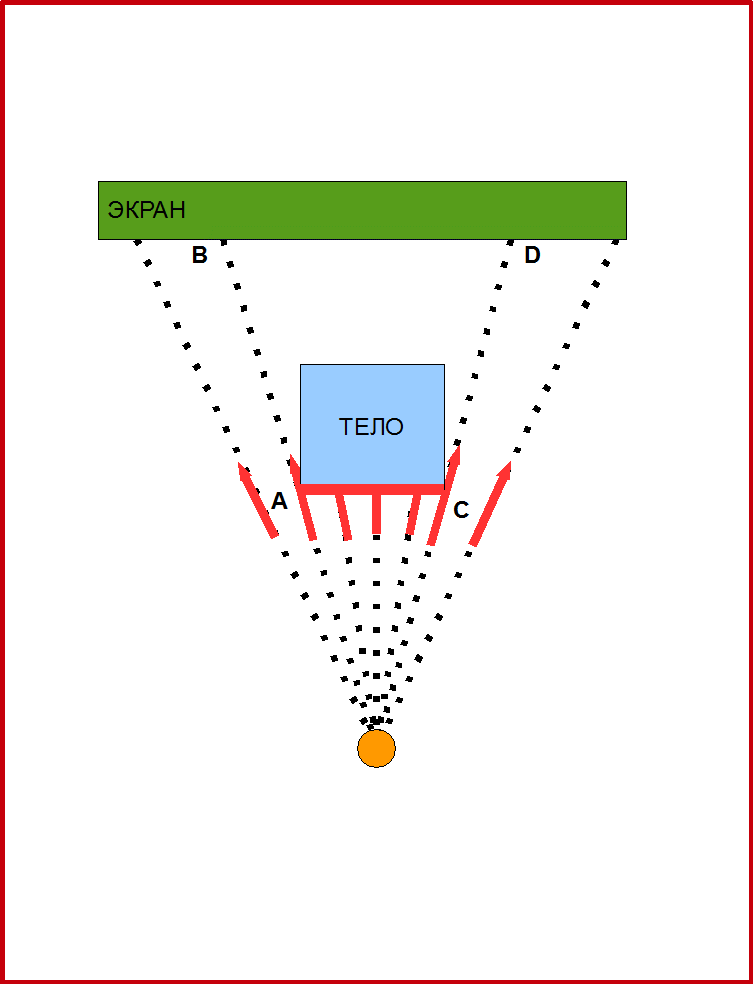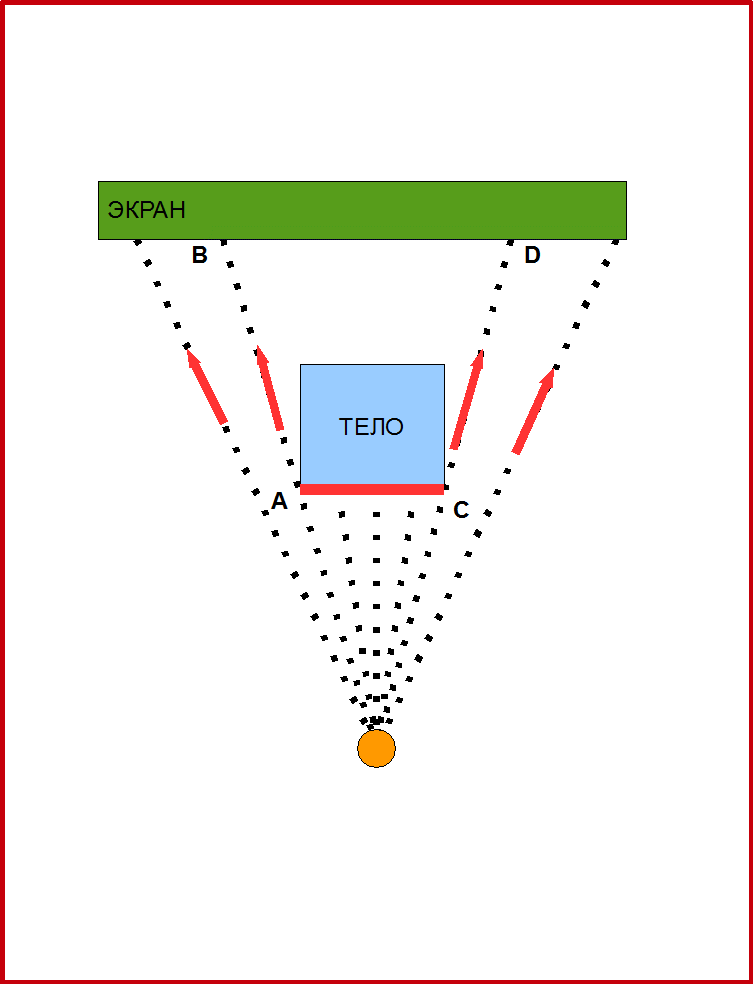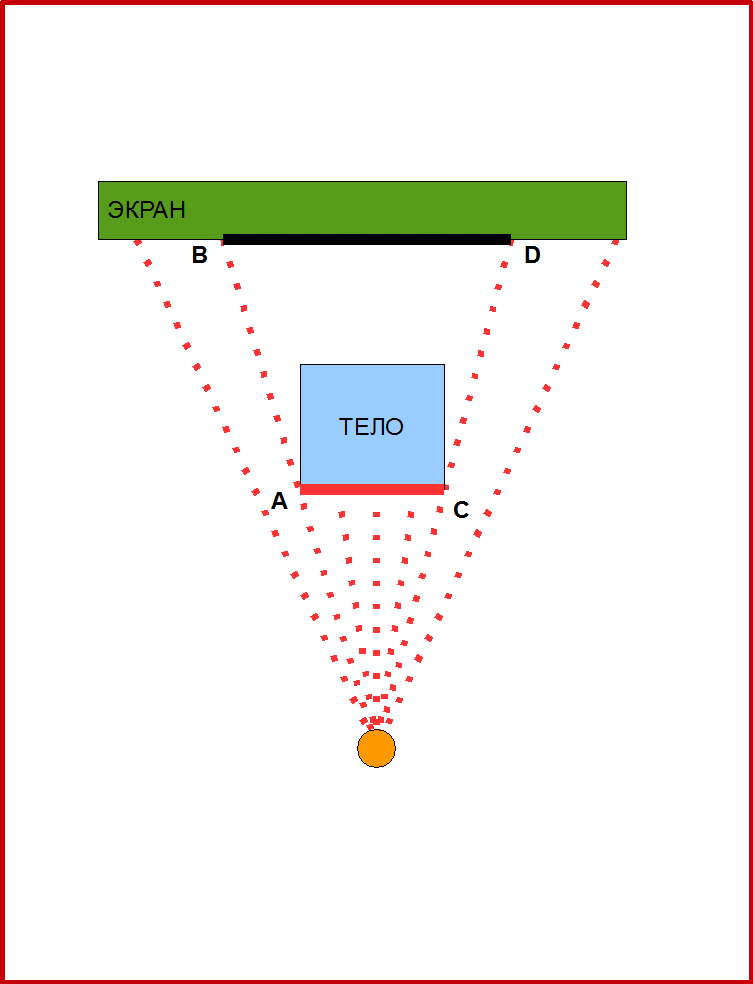
Рис.1. Принцип работы проектора с точечным источником света. Такой проектор создаёт перспективную проекцию. Размеры при такой проекции меняются. Например, точки А и С на теле преобразуются в точки B и D на экране. Отрезок BD проекции больше исходного отрезка АС.
И в полученной проекции (Рис.2), тени параллельных прямых (на рисунке параллельные прямые обозначены красным цветом, а их тени черным) тоже стремятся пройти через общую точку- точку схода (т.К на рисунке). Правда они через нее так и не пройдут, а будут только стремиться к ней.
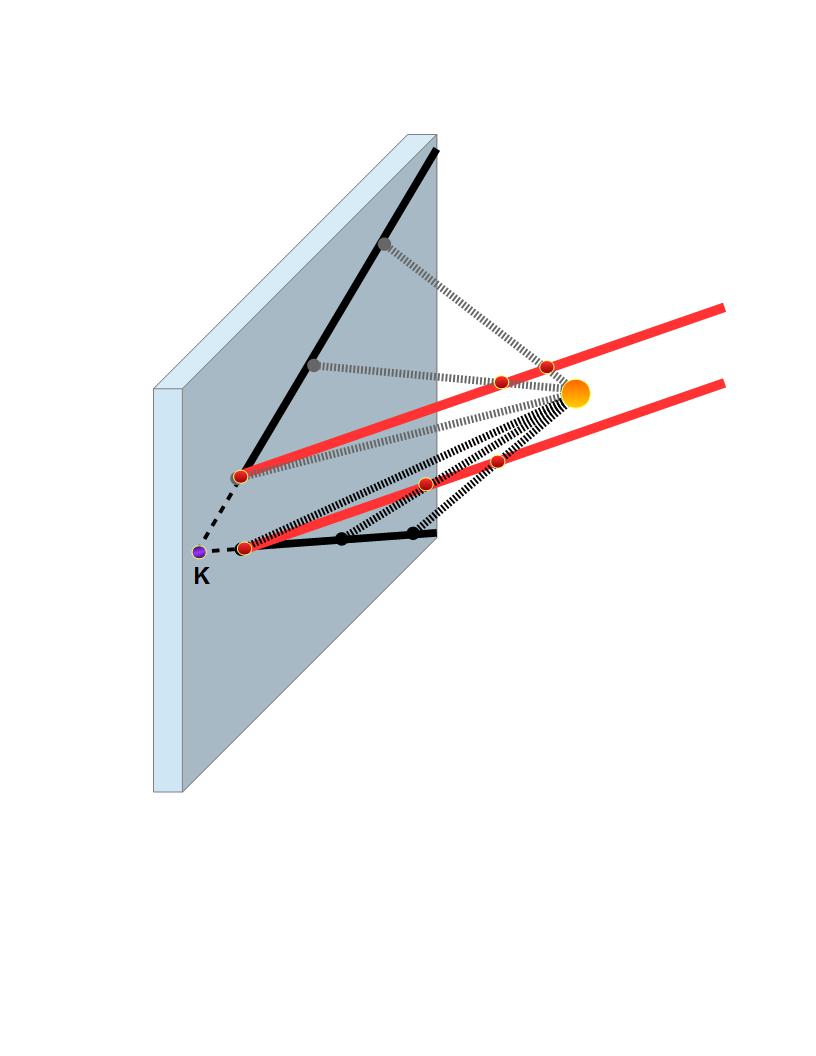
Рис.2. Перспективная проекция параллельных прямых на плоскость. Источник света показан кружочком оранжевого цвета. Красным цветом показаны пораллельные прямые. Черные лучи- это тени красных. Чтобы объяснить, как они получаются, проведены несколько лучей из источника света. Лучи обозначены мелкими штриховыми линиями. Сначала, лучи проходят через точки на параллельных прямых. Эти точки отмечены красным цветом. Затем лучи проецируют красные точки в черные точки проекционной плоскости. Черные точки лежат на черных лучах. Аналогично можно было бы поступить и для других точек красных прямых. Поэтому черные лучи - это проекции красных. Получившиеся проекции красных прямых (тени красных прямых) при продлении пересекаются в т.К.(в курсе геометрии мы докажем это).
Интересно, что в точке К будут сходится проекции всех прямых параллельных красным. Говорят, что точка К будет точкой пересечения проекций данного семейства параллельных прямых. Если же мы возьмем другое семейство параллельных прямых, то у их проекций на плоскость будет другая точка пересечения. Если параллельные прямые будет ещё параллельны плоскости проекции (т. е. они не пересекаются с плоскостью), то их проекции-тени тоже будут параллельными. Вы можете сами в этом убедится, поиграв с проекциями параллельных реек (проволочек, брусьев, струн) и вашим простейшим проектором. Придумайте сами, как лучше это сделать.
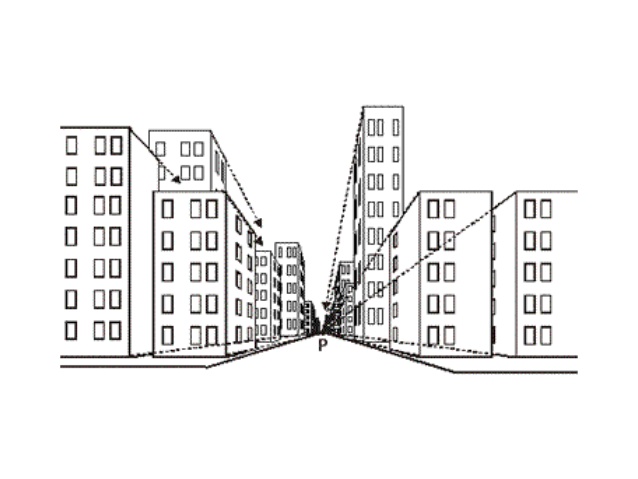
С перспективными (или еще их называют центральными) проекциями вы хорошо знакомы по картинам и фотографиям. Рис. 3 приводит пример типичных рисунков с одной и двумя точками схода.
б)
Рис 3. а) Рисунок с перспективой (точка схода Р). Как хорошо видно все параллельные линии крыш, тротуаров, этажей сходятся в т.Р. В то же время линии крыш, этажей, тротуаров параллельных плоскости рисунка (смотрящих на нас) остаются параллельными и на самом рисунке, и точки пересечения не имеют.
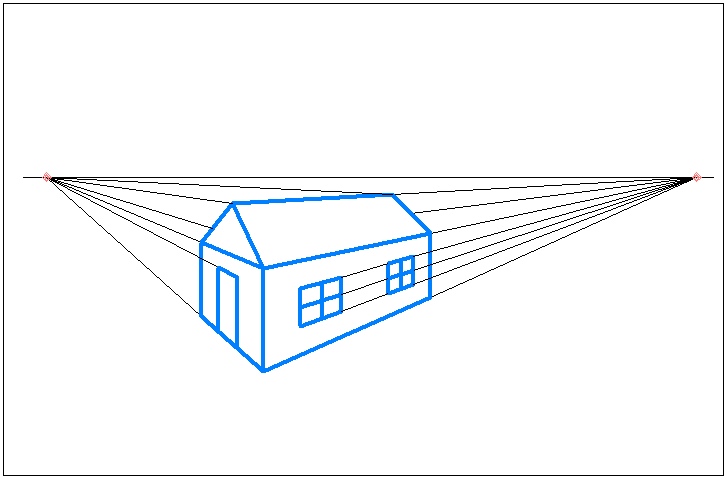
б) Рисунок с двумя точками схода. Здесь видны два исходных семейства параллельных прямых. У каждого из них своя точка схода.
Наглядным примером параллельной проекции является детская игрушка, показанная на фотографии 4а. Принцип её работы можно понять из фотографии 4б.

а) б)
Рис. 4. а) 3-х мерный игольчатый рельеф-воспроизводитель; б) принцип работы игольчатого рельеф-воспроизводителя основан на смещении параллельных красных иголок вслед за изменениями рельефа. Здесь можно посмотреть видео о том, как можно сделать такой рельеф-воспроизводитель (pin art toy), и как он работает: https://youtu.be/wFeLveRps8s , или здесь: https://youtu.be/0YctQT__GLg
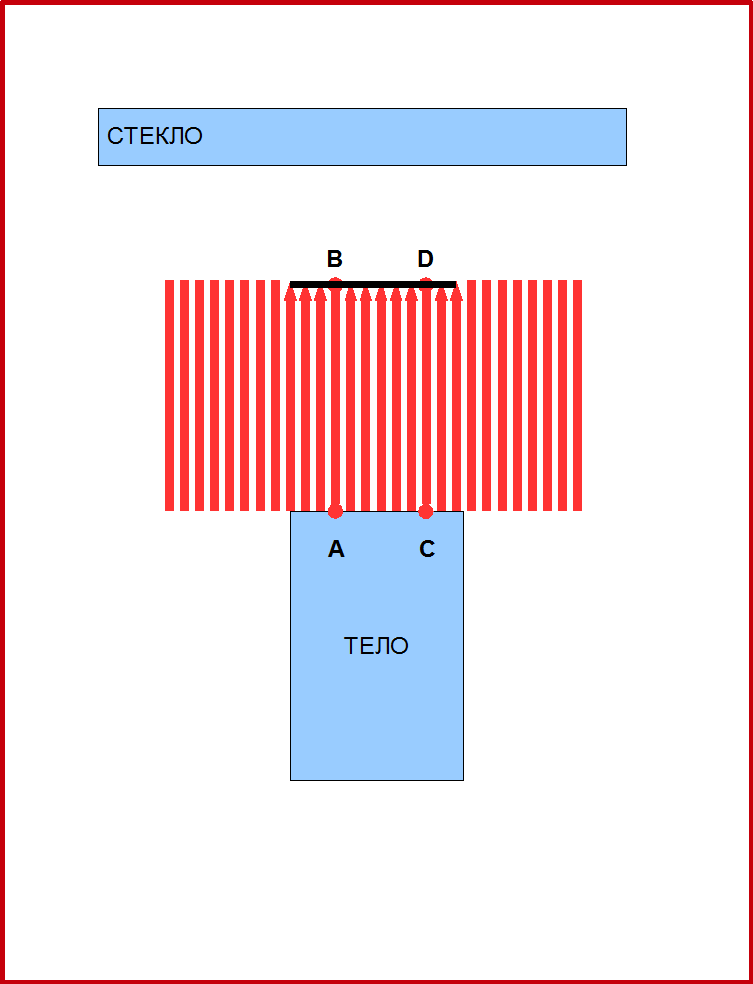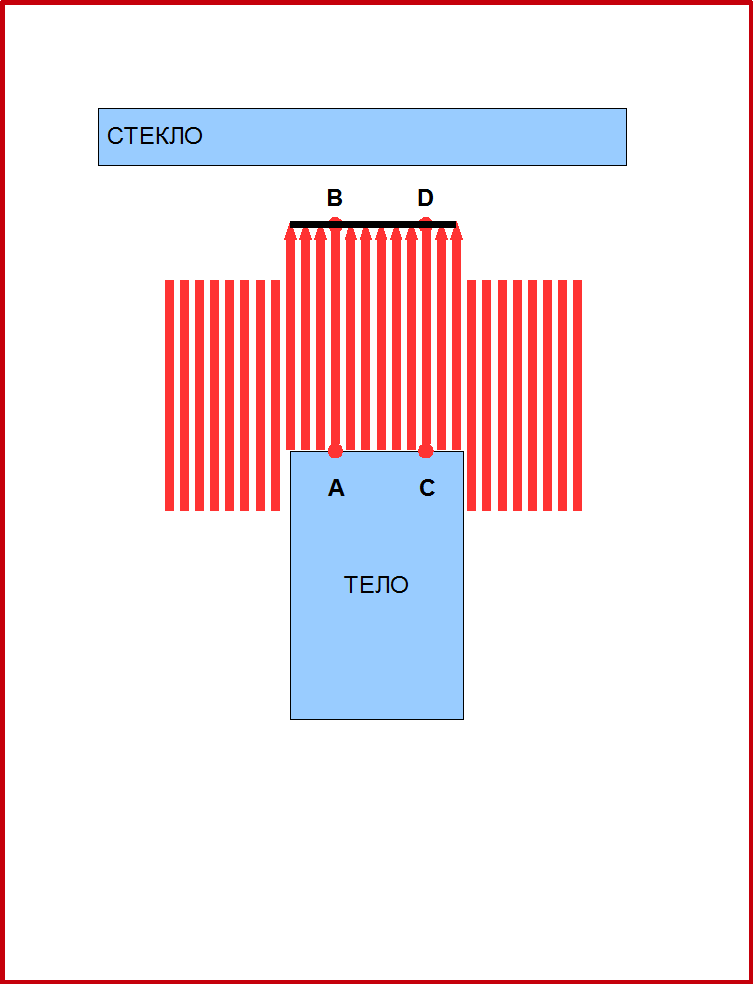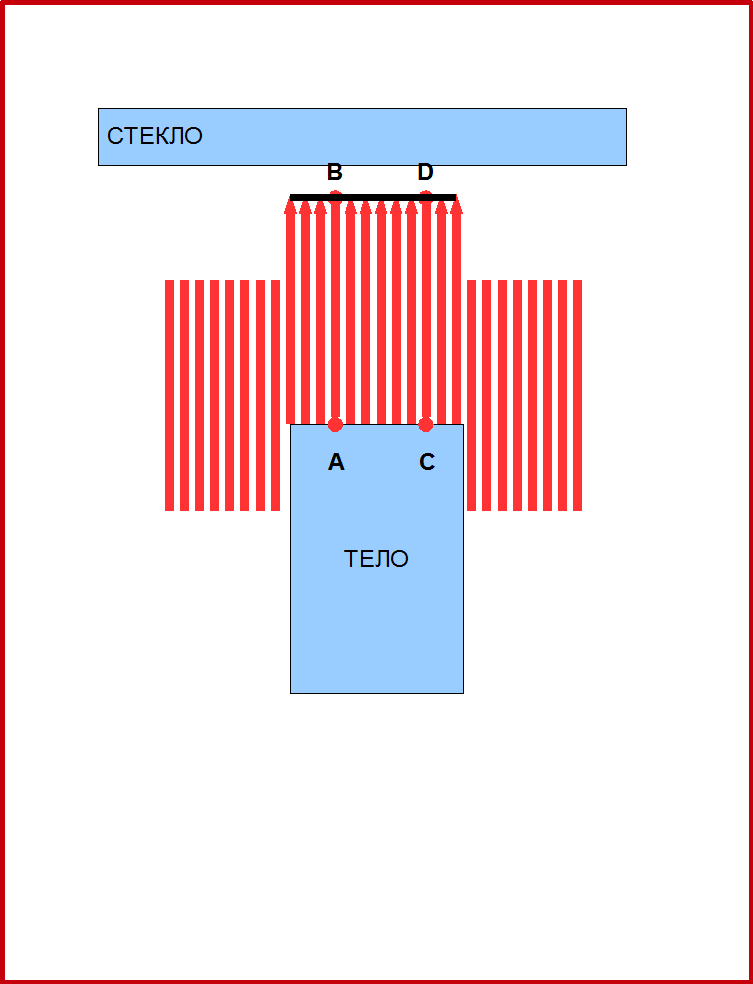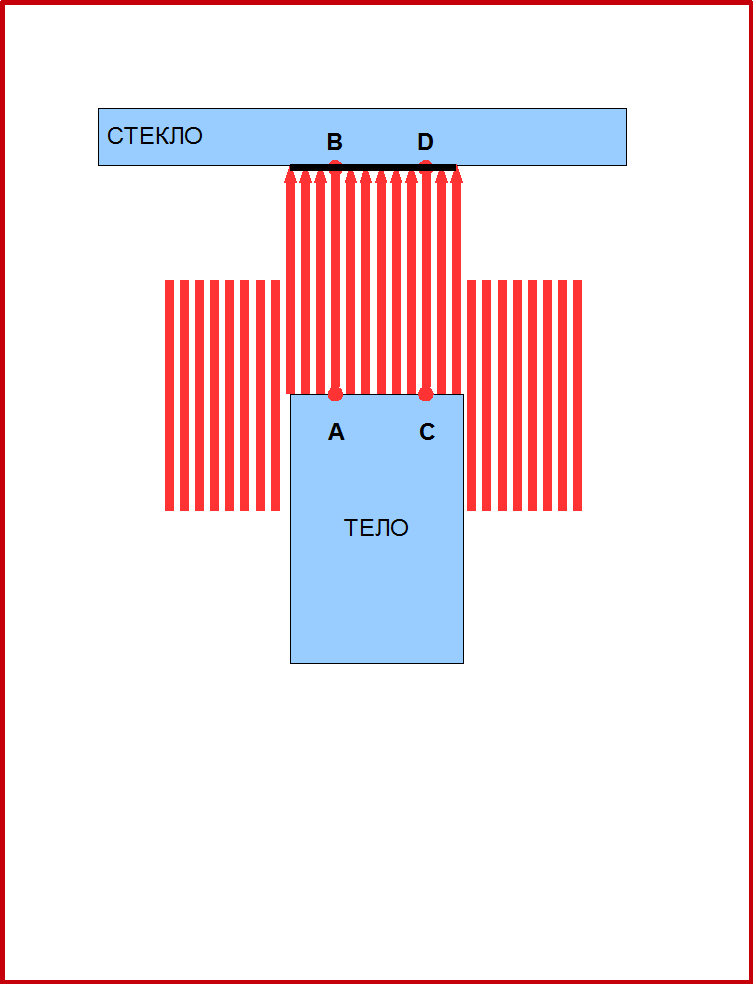
Рис.5. Принцип работы 3D рельеф-воспроизводителя.
На Рис.5, принцип работы игрушки показан схематично. Когда тело поднимается, то оно толкает иголки, и они тоже поднимаются. При этом каждой точке А тела соответствует своя точка В на поверхности иголок. Таким образом поверхность тела, как бы преобразуется в поверхность иголок. Можно сказать, что когда поверхность иголок касается стекла, поверхность тела проецируется в точки поверхности стекла. При такой проекции каждая точка тела проецируется вдоль соответствующей иголки, и иголки будут линиями проекции. Это будет параллельная проекция, поскольку все линии проекций параллельны. Более того, это будет ортогональная проекция, поскольку проекционные линии (иголки) перпендикулярны поверхности стекла, на которую мы проецируем тело. Особенностью ортогональных проекций являются: 1) сохранение расстояний при проецировании; и 2) параллельные прямые всегда преобразуются в параллельные. Например, на рисунке 5, отрезок АС проецируется в отрезок BD. Длины отрезков равны. Вы наверное уже догадались, где вы встречались с ортогональными проекциями. Таким примером были проекции технических чертежей с масштабом 1:1. Рис.6 показывает другие примеры ортогональных проекций выполненных с помощью такого проектора.

Рис.6. Примеры ортогональных проекций выполненных с помощью 3D рельеф-воспроизводителя.
Параллельная проекция сохраняет параллельность прямых при проекции, как и ортогональная проекция, но может менять размеры отрезков и тел. Отличия параллельной и перспективной проекций показаны на рисунке 7.
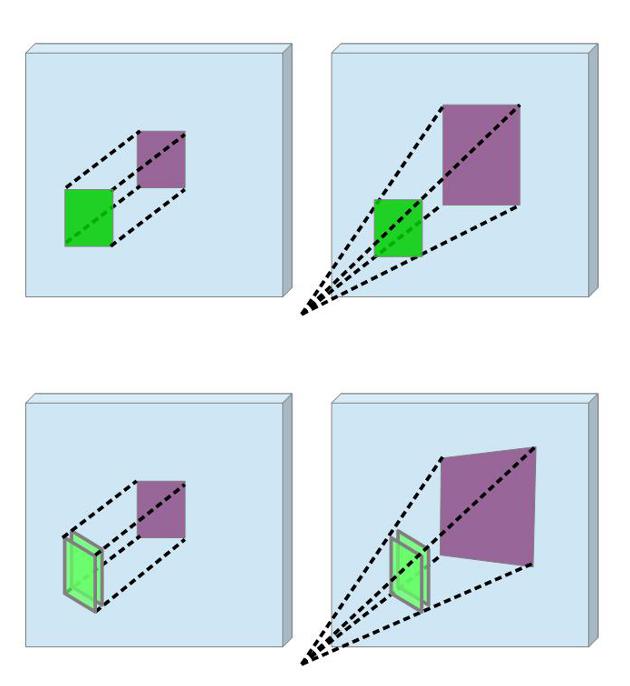
Рис.7. Слева- параллельная проекция; справа- перспективная проекция.
Общее для параллельных и перспективных проекций является то, что они прямые линии преобразуют в прямые, не искривляя их. Это линейные преобразования. Они могут менять размеры тел, но любая прямая преобразуется в прямую.
II. Основные математические понятия, которые нам необходимо знать сейчас.
Итак физика занимается изучением явлений природы. Что мы называем явлениями? Под этим термином мы понимаем преобразования в природе, в результате которых меняются положение тел в пространстве и/или характеристики изучаемого объекта, например его температура, размеры, вес. Поэтому для описания происходящих явлений нам очень важно знать, что такое преобразование. С одним из примеров преобразований, проецированием, вы только что познакомились. При проецировании одна фигура преобразуется в другую.
Как следует из самого названия, преобразование описывает любое явление, когда что-либо преобразуется. На языке математики, это же звучит немного по другому.
Во- первых, неопределенное понятие «что-либо», заменяется на более конкретное «множество точек». При этом под словом точка может пониматься все что угодно: числа, мячи, ячейки таблицы, точки тени, способы бега, цвета радуги и т.д. Во-вторых, преобразование означает преобразование этой точки в другую точку. Преобразовав все точки исходного множества в «другие», мы таким образом создаём новое множество преобразованных точек (Рис.8):
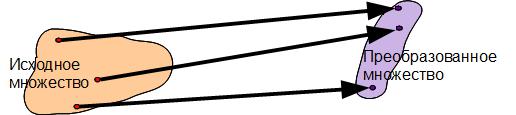
Рис.8. Преобразование исходного множества точек в преобразованное.
Посмотрим, что такое преобразование на примере обжаривания курицы (Рис.9). Стрелками показано в какие точки преобразуются отдельно взятые точки на исходной тушке. Понятно, что для примера таких точек можно было бы взять много больше. Математик скажет, что вся тушка курицы состоит из бесконечно маленьких точек, и таких точек бесконечно много. Если же физик станет моделировать поведение тушки при обжаривании, то он скажет, что каждая такая точка заключает в себя очень маленький объем тушки курицы. И чем меньше этот объем, тем больше таких точек, тем точнее мы сможем рассказать, что происходит при преобразовании.
Вообще преобразовываться могут не только материальные точки и их координаты. Преобразовываться могут и разные величины характеризующие технологические процессы или состояние тела. Например в случае с курицей, это могла бы быть температура тушки в отдельных точках в разные моменты времени обжаривания.

Рис.9. Преобразования при обжаривании курицы

Рис.10. Преобразования человека, выполненные с помощью компьютерной графики.
III. Функции
Фотография на Рис.10 иллюстрирует виртуальные преобразования человека, осуществленные с помощью компьютерной графики. Для примера, показано преобразование всего одной точки изображения человека. Даже в процессе создания самого простого изображения на компьютере, например того, что вы видите перед собой, каждая точка-пиксель исходной фотографии преобразуется несколько раз перед тем, как вы увидите её на экране монитора.
Эти две фотографии (Рис.11) бегущего человека показывают преобразование положения точек тела бегуна в пространстве. На первом снимке для примера взята опять только пара точек. Вы можете определить преобразования остальных точек тела сами. Вторая фотография показывает преобразование полосок-меток на одежде бегуна в пространстве во время бега. Таким образом изучают движение частей тела во время бега. Знание того, как преобразуется их положение относительно друг друга, затем используется в компьютерной графике при рисовании мультфильмов и создании современных художественных фильмов.
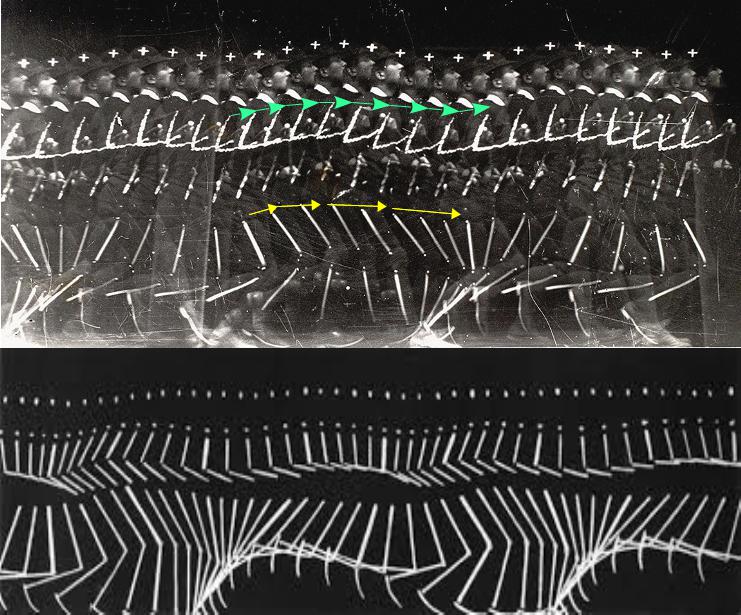
Рис.11. Изменения положения частей тела человека при беге.
Как именно каждая точка исходного множества преобразуется в точку преобразованного множества — определяется функцией, которая задаёт это преобразование.
Поскольку функция описывает преобразования исходного множества, то сначала всегда надо определить это исходное множество. Это может быть множество точек тела, которое мы изучаем. Или это может быть множество различных свойств этих точек. Например, их температура, или их координаты, или их вес. На языке функций, исходное множество называется множеством определения функции. А множество в которое оно преобразуется, называется множеством значений функции.
Если каждой точке области определения функции соответствует только одна точка области значений функции, то говорят, что функция однозначная.
Если преобразование ставит каждой точке исходного множества в соответствие одну только точку , и если мы будем преобразовывать область значений в обратном направлении в область определения и это преобразование опять будет однозначным, то говорят, что данное преобразование взаимно однозначное.
Например, на рисунке 12а две точки преобразуются в одну и ту же точку в области значений. Это однозначное преобразование, но не взаимно однозначное. Ведь теперь для обратного преобразования, этой одной точке области значений будет соответствовать две разные точки определения. А если две точки преобразуется в две разные точки как на рисунке 12б, то это будет взаимно однозначным преобразованием.
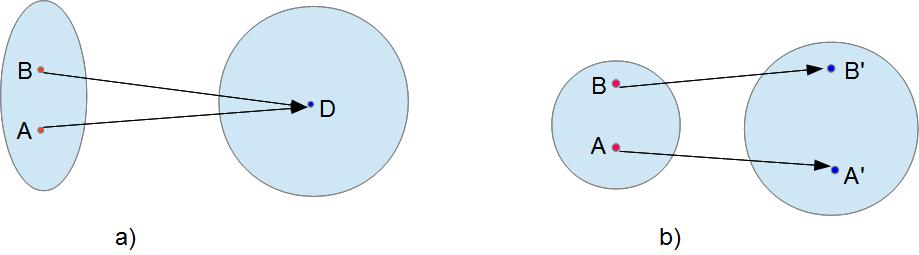
Рис.12.
Рисунок 13 показывает еще один пример однозначной функции. Здесь каждой точке исходного множества красных точек можно поставить в соответствие свою и только одну синею точку из множества значений функции. Например, на рисунке показаны три красных точки А,В и С, и три синих А', B' и C' в которые они преобразовались. Но мы могли бы взять и любые другие точки из исходного множества, и точно так же найти точки в которые они преобразовались. То есть, все точки преобразованного множества можно соединить с соответствующими точками исходного множества, как это показано для точек А, В и С.
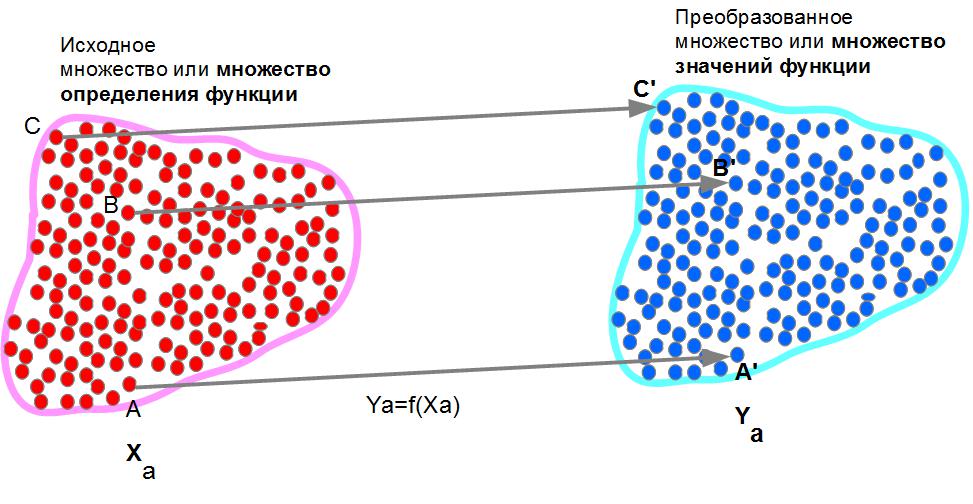
Рис. 13. Однозначное преобразование.
Значит, все точки можно разбить на пары связанных между собой точек. Так для выделенных точек, это будут пары АА' , BB' и CC'. Линия, которая их соединяет, будет обозначать правило, по которому мы получили преобразованную точку из исходной.
Например, если мы получили синие точки просто параллельным перемещением (при параллельном перемещении все точки перемещаются вдоль параллельных прямых, как при параллельной проекции, но на одинаковое расстояние), то эти линии будут траекториями движения точек.
Но это может быть и любое другое правило. Например, преобразование может обозначать охлаждение точек. Допустим, в исходном множестве точки имели комнатную температуру, а затем мы их охладили до температуры замерзания воды. При этом точки могут оставаться на своих местах, но их температура станет 0С.
Преобразование может обозначать и перекрашивание точек из красного в синий цвет.
Каждое из перечисленных преобразований задается своей функцией, которая каждой точке исходного множества ставит в соответствие точку преобразованного множества. Этими функциями будут в одном случае- функция перемещения, в другом- функция охлаждения, в третьем- функция окраски.
Очевидно, что такие пары точек AA', BB', CC',...., сами будут характеризовать функцию преобразования А в A', B в B' , C в C', ...... Определив эти пары, мы узнаем каким было преобразование.
Функция- это понятие математическое. А для чего они нужны нам? Дело в том, что физика изучает явления природы. Но любое природное явление связано с тем или иным преобразованием.
Например, возьмем дождь. Это явление связано с конденсацией водяного пара. При этом молекулы воды испытывают преобразование: переходят из газообразного состояния в жидкое.
В случае падения тел, например падение яблока с яблони, яблоко перемещается с ветки на землю под действием силы притяжения Земли. Это явление связано с преобразованием местоположения яблока.
Для объяснения явлений природы, мы должны будем использовать самые разные функции. Поэтому, мы должны научиться определять функции, которые задают то или иное преобразование. Как это сделать? Как задать математически пары точек АA', BB', CC' …. ?
Очевидно, для этого надо научиться характеризовать точки из областей определения и значений функции математически, т. е. с помощью чисел.
Сделать это очень просто. Как уже сказали, функции связаны с явлениями природы. А вы уже знаете, что каждое природное явление связано с изменениями тех или иных свойств. Например, с изменением положения тел, температуры тел, их массы и так далее. Поэтому будем характеризовать точки либо их координатами, либо их температурами, либо их массой или другими величинами, которые подойдут для описания исследуемого явления природы. Обозначим через Х значение любой из таких величин для точек области определения, а через Y значения соответствующей величины для точек области значений, которые мы измеряем при наблюдении явления. Обозначим через Xa значение величины Х для точки А, и через Ya значение величиныY для точки A' (см. Рис.13). Аналогично определим XbYb для пары BB', XcYc для пары CC', и так далее.
Например, мы исследуем нагревание воздуха в закрытом сосуде и смотрим за изменением давления газа, чтобы определить при какой температуре давление станет опасным и сосуд может взорваться. В этом случае, Х будет температура газа, а Y давление газа, а значения пар XаYа, XbYb, XсYс ... образуют таблицу показанную на Рис.14. Пары XаYа, XbYb, XсYс... этой таблицы определяют функцию изменения давления газа от его температуры. Левая колонка таблица- это область определения функции, а правая- область ее значений.
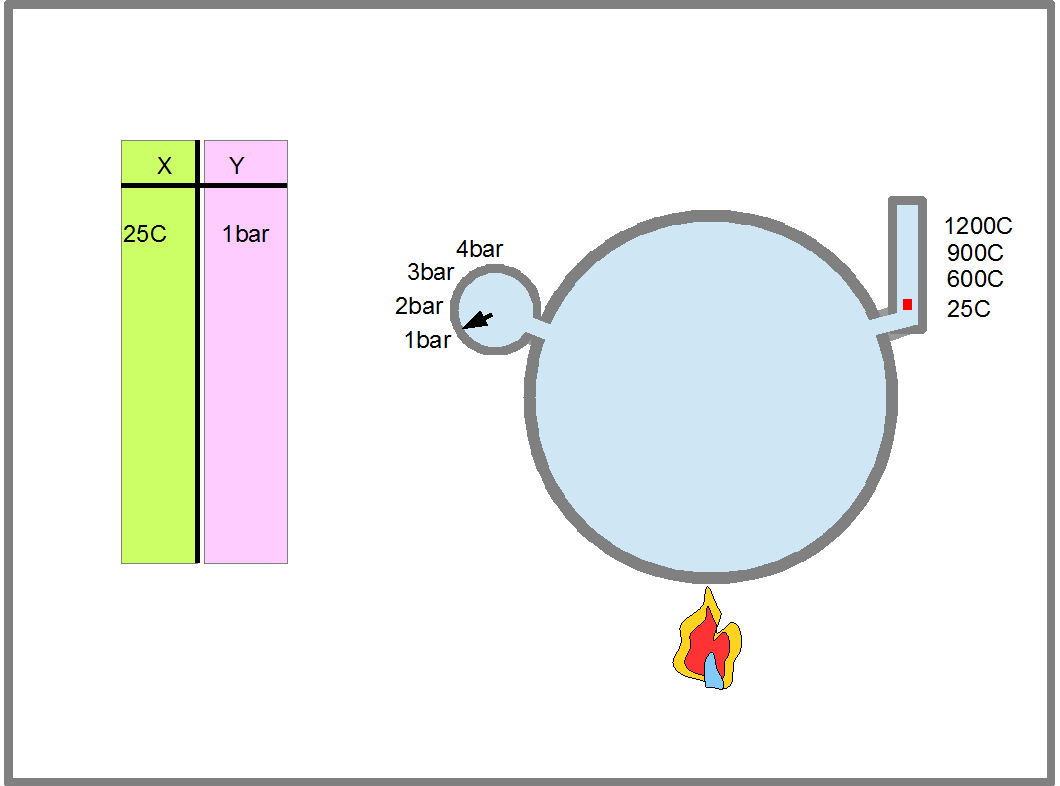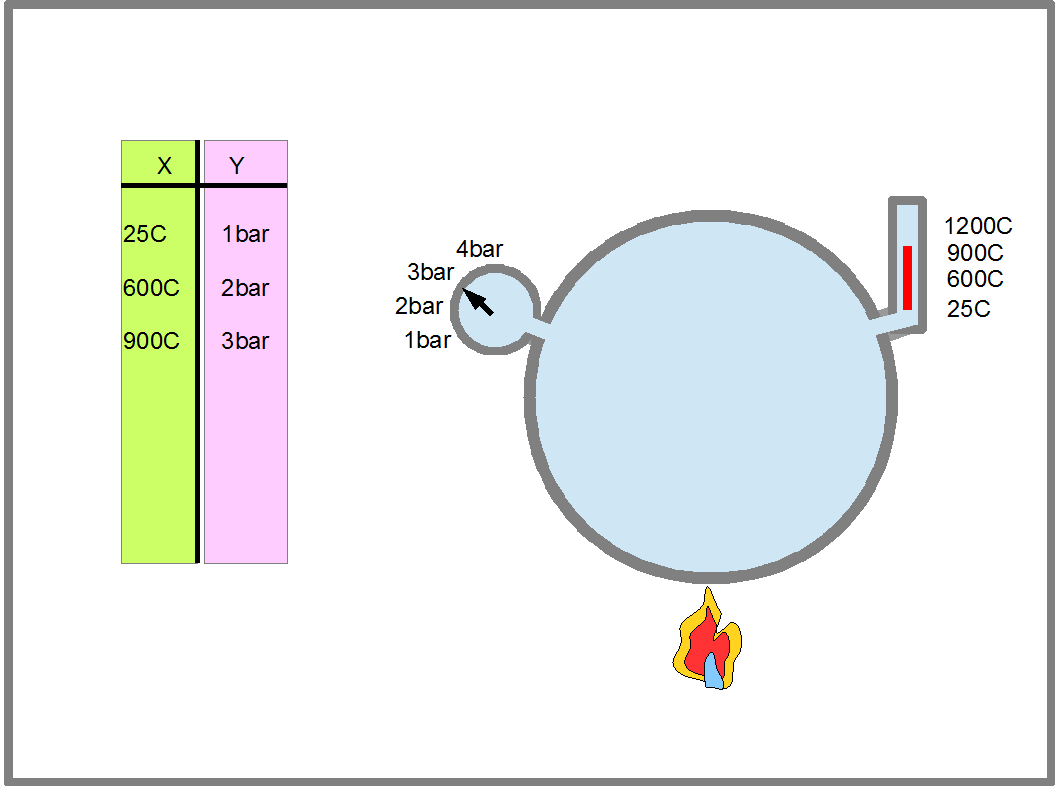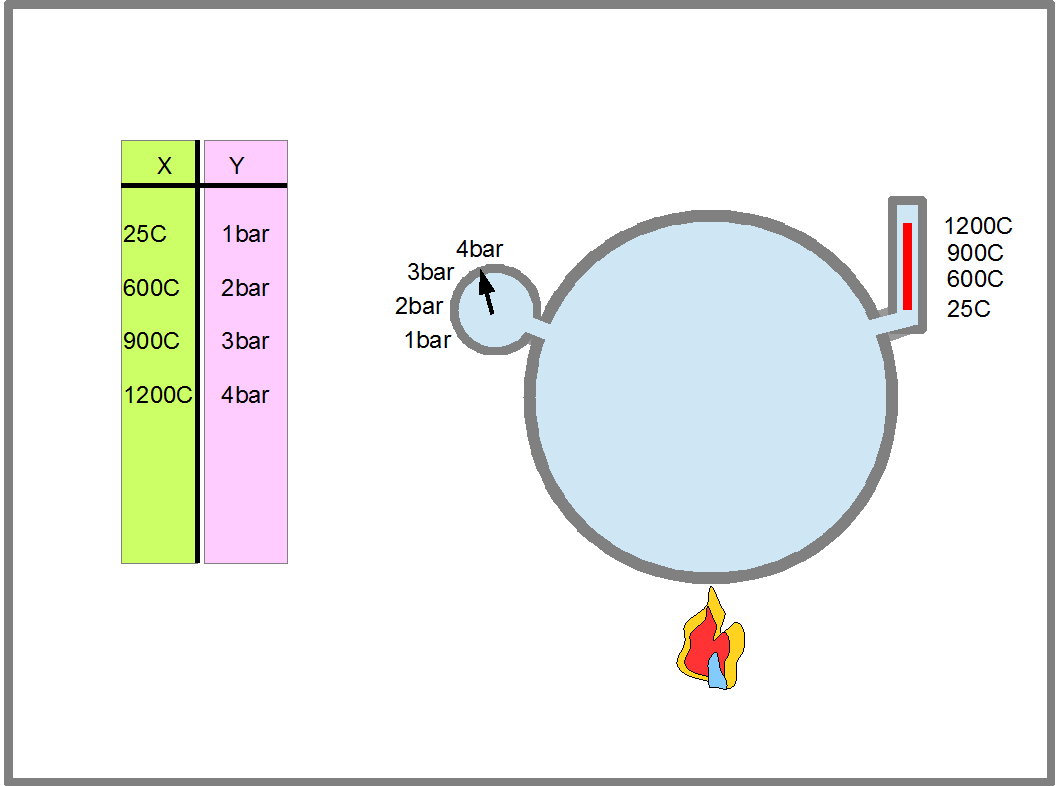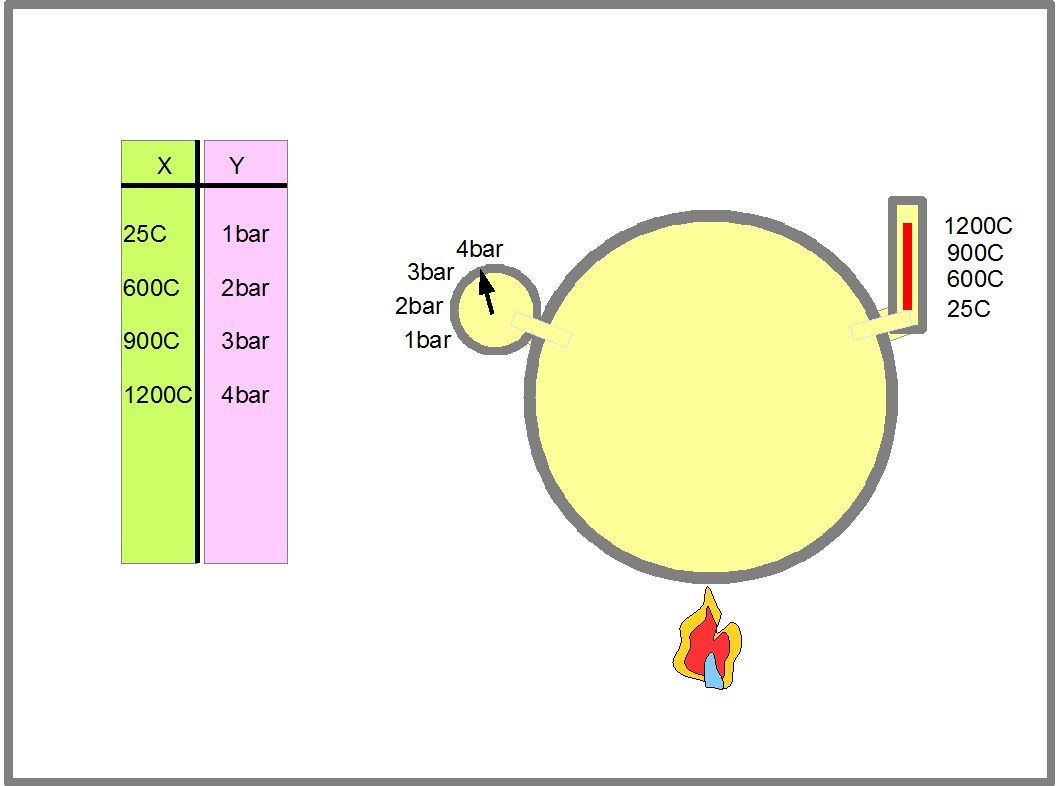
Рис.14. На рисунке изображено, что происходит с давлением газа в замкнутом объеме при нагреве. Впервые явление роста давления газа при нагреве было описано французским ученым Шарлем в 1787году. Результаты измерений заносятся в таблицу. Полученные пары чисел XаYа, XbYb, XсYс... этой таблицы определяют функцию изменения давления газа от его температуры. Первым, кто правильно определил эту функцию, был французский ученый Гей-Люссак. в 1802 году спустя 15 лет после открытия явления Шарлем. Левая колонка таблицы- это область определения функции, а правая- область ее значений. В математике, и в программировании вместо обозначений отдельных точек множества буквами алфавита, точкам могут присваивать порядковые номера. С такой нумерацией вы часто сталкиваетесь в жизни. Например, все дома на вашей улице имеют свой порадковый номер. Солдаты в строю называют свой порядковый номер по команде "По порядку расчитайсь". В этом случае, вместо обозначений Xа, Xb, Xс... и Yа, Yb, Yс... часто используют обозначения X1, X2, X3... и Y1, Y2, Y3... . Например X4=1200C, a Y4=4bar.
Или мы хотим определить с какой скоростью камень ударится о Землю, если он падает с высоты второго этажа. Тогда нам надо найти функцию скорости падения от камня от времени падения, или скорость падения камня от расстояния камня до Земли. Для этого, мы можем мысленно разбить падение камня на отдельные отрезки-моменты времени и составить таблицу, в которой время прохождения определенных точек примем за Х, а расстояние этих точек до Земли примем за Y (Рис.15). Мы получим расстояние камня до Земли, как функцию от времени падения.
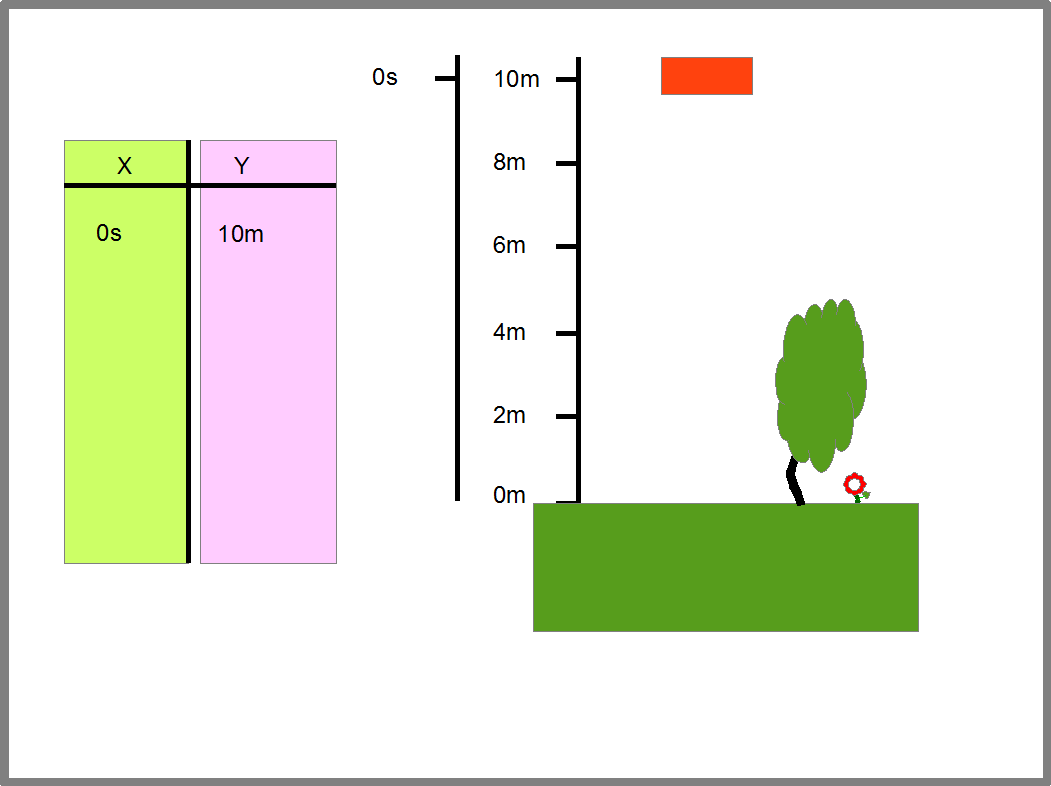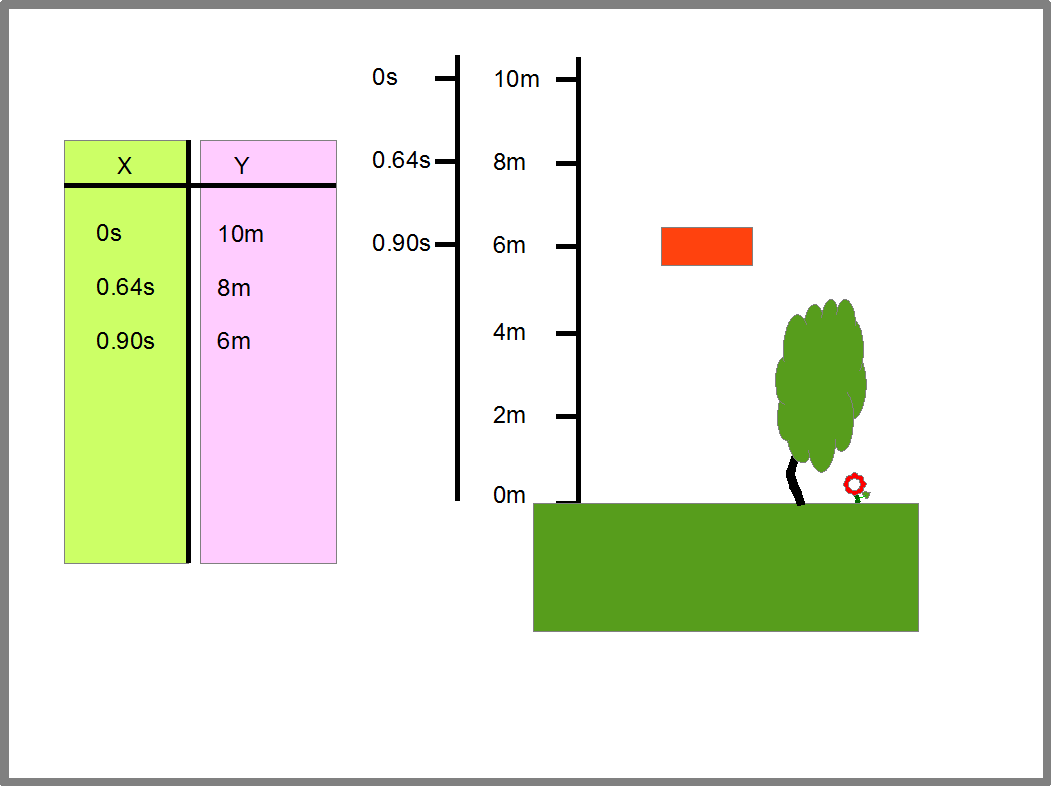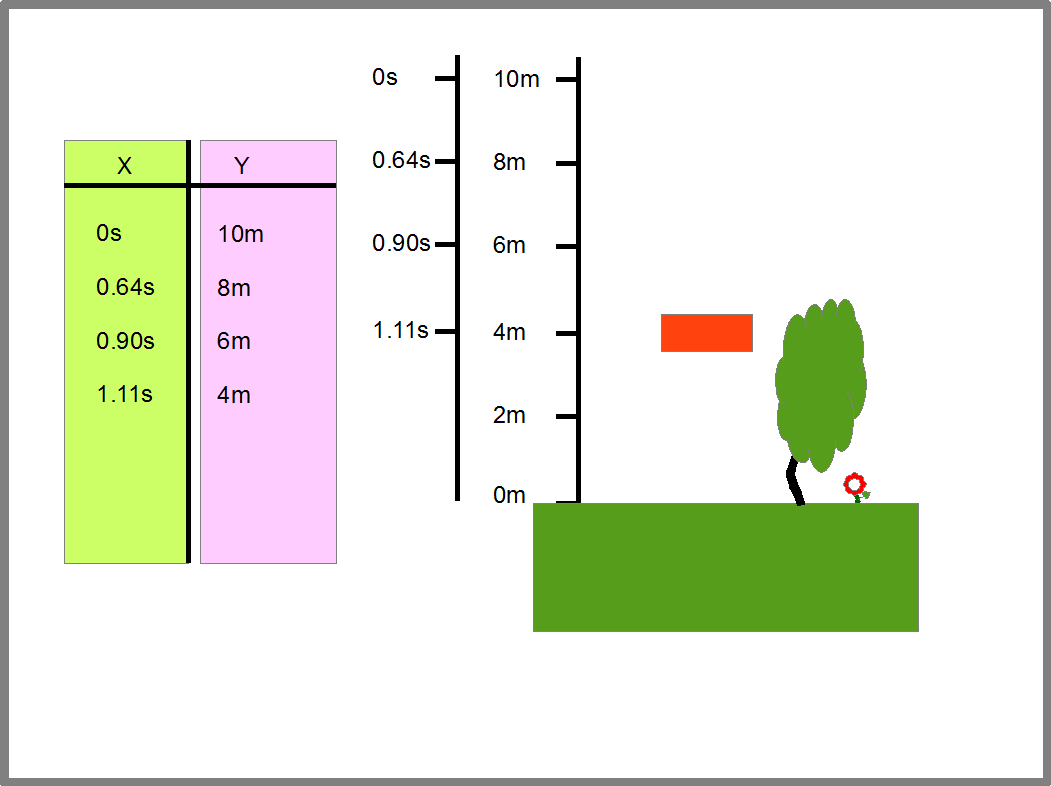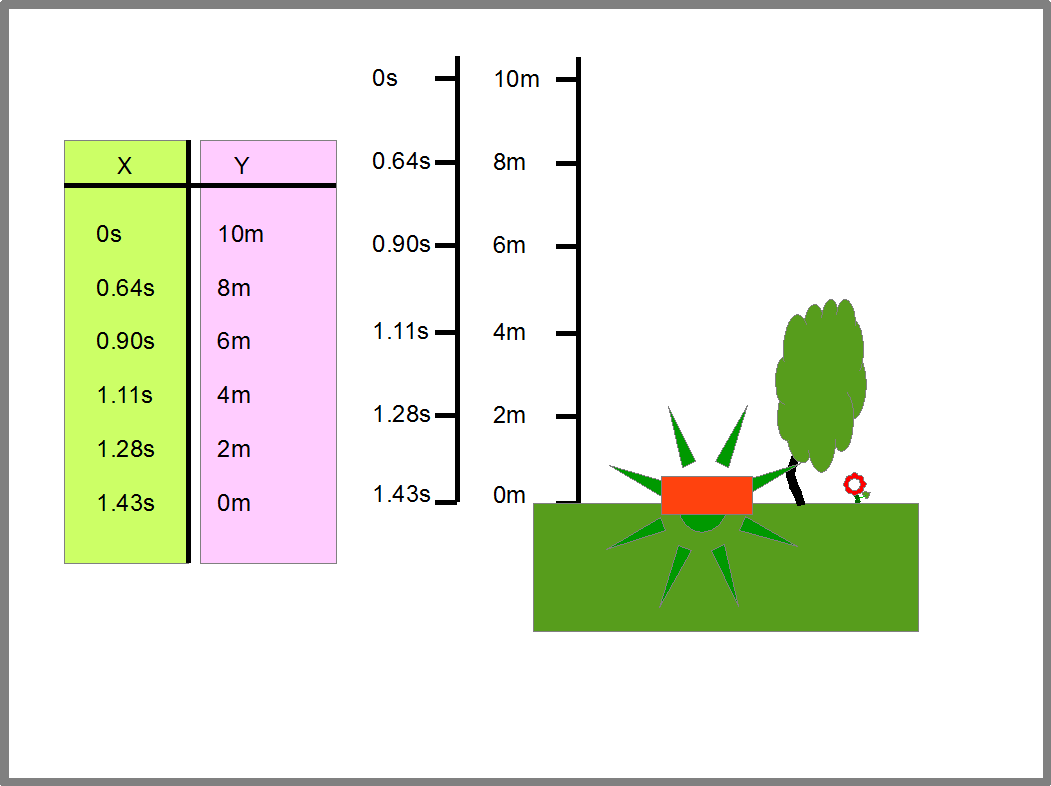
Рис.15
Эта функция дает нам интервалы времени и расстояние, которое пролетает камень за эти интервалы. Отсюда мы можем найти скорость камня за те же временные интервалы, ведь скорость равна расстоянию деленному на время, в течении которого камень пролетает это расстояние. Определив пары «время падения- соответствующая ему скорость камня», мы сможем заполнить таблицу, которая задаст нам функцию скорости камня от времени падения (Рис.16).
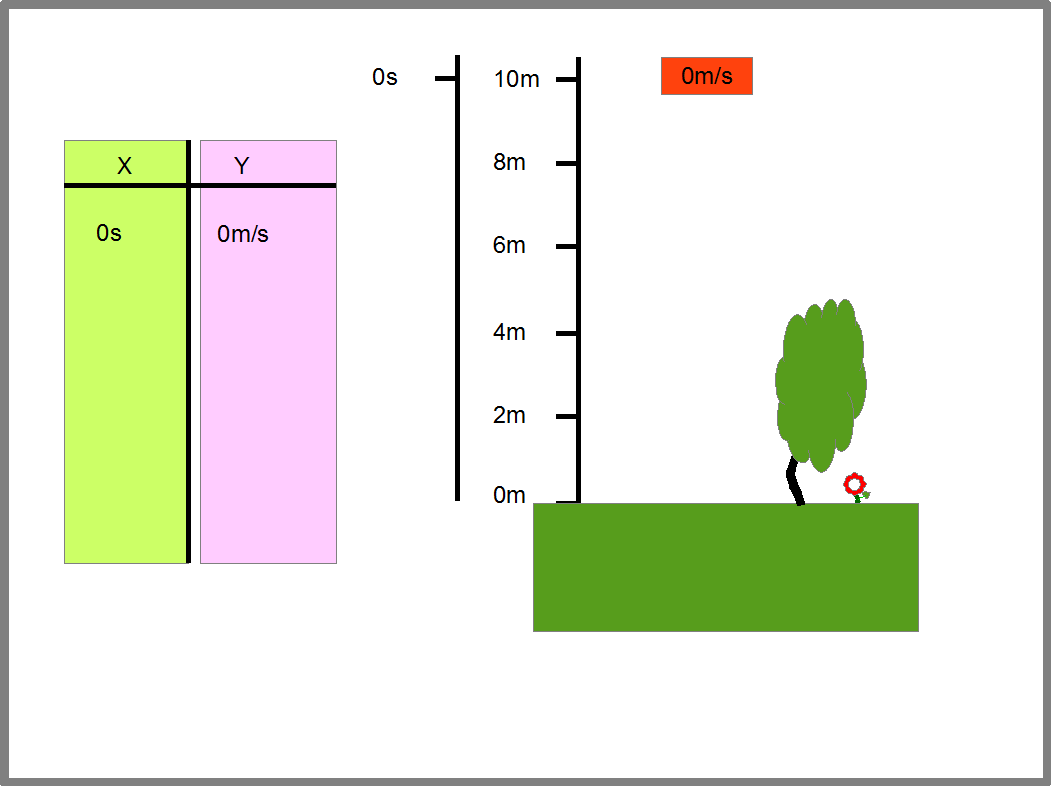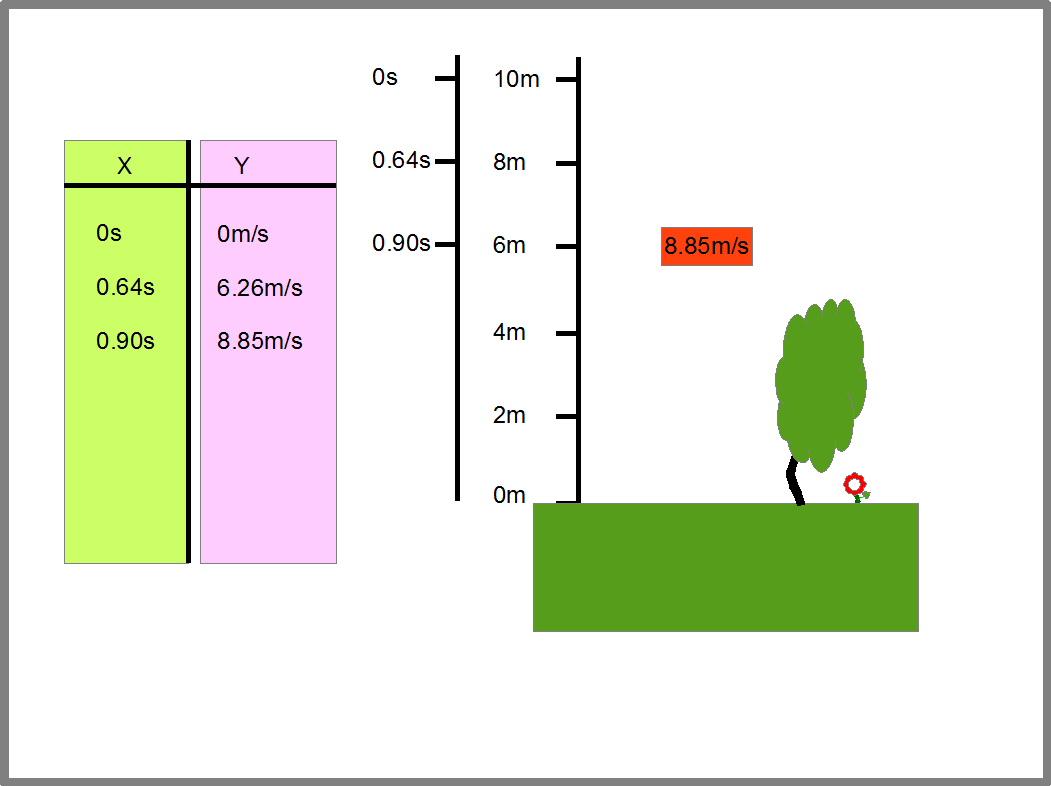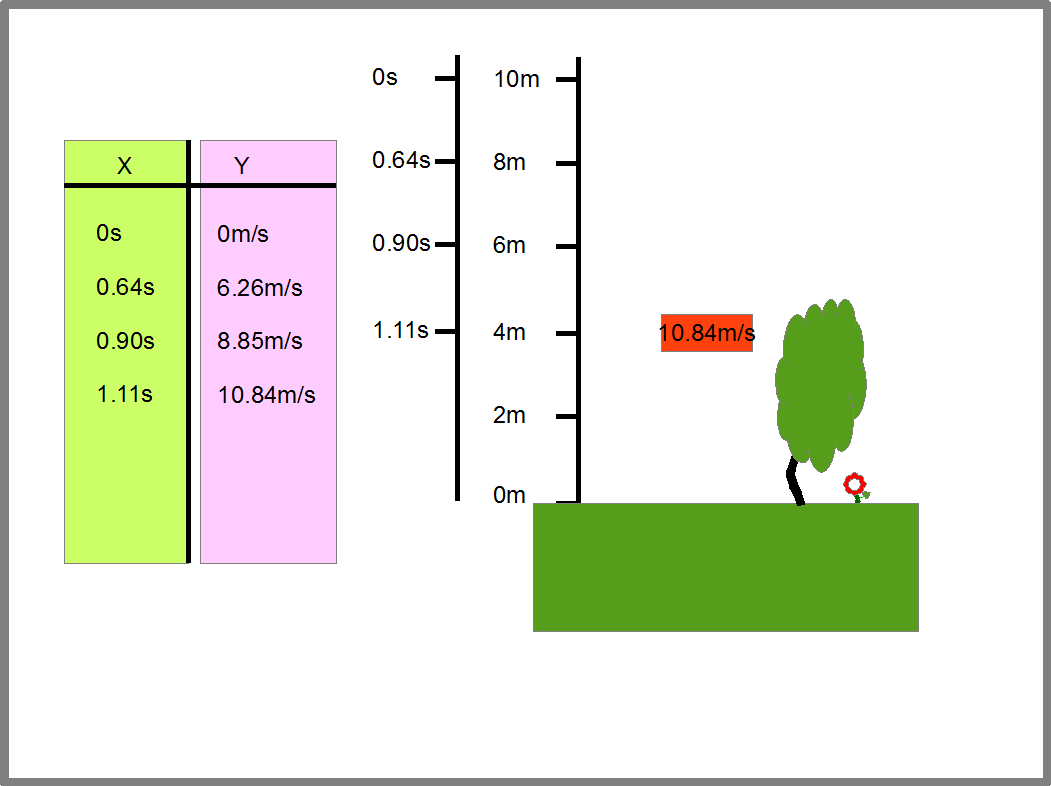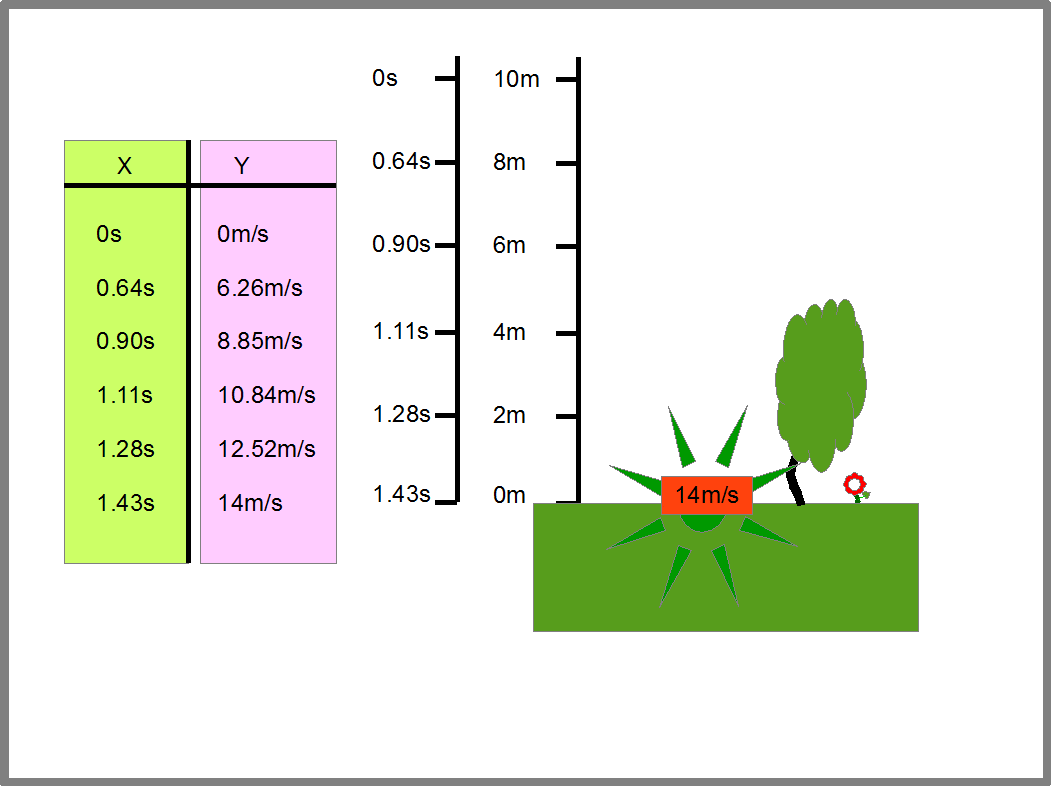
Рис.16
Эту же функцию мы можем представить в виде графика (Рис.17). В нем точки оси Х показывают время падения камня, а точки оси Y- скорость камня в соответствующий момент времени.
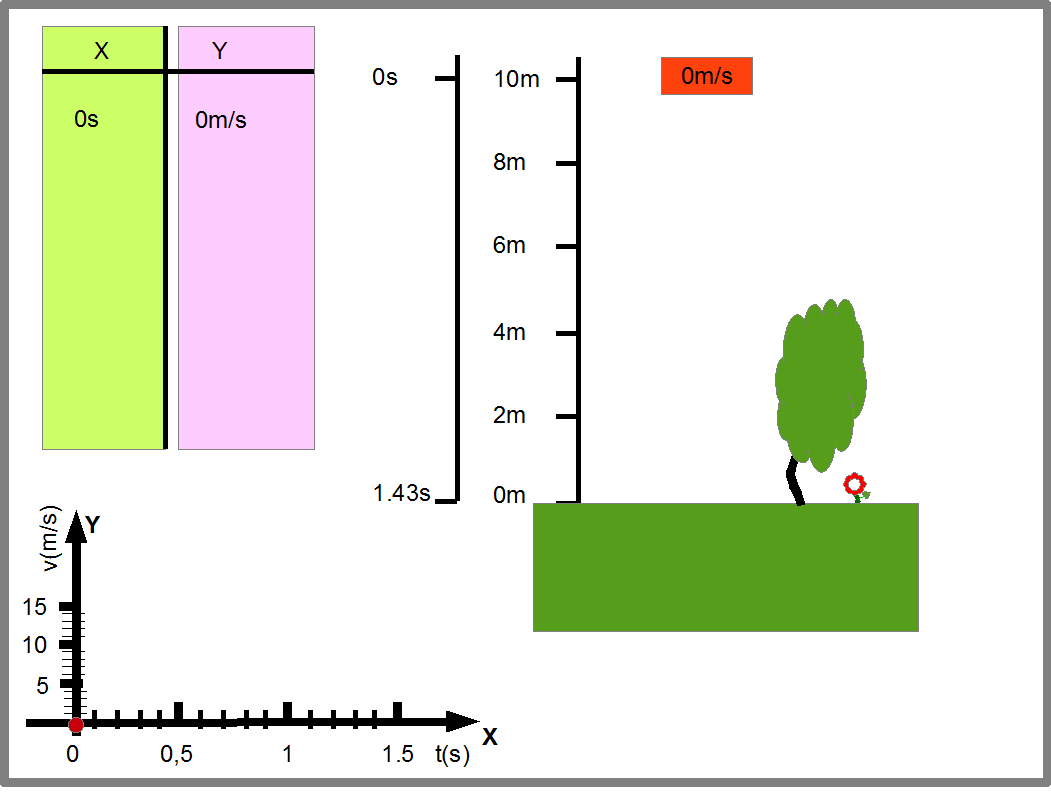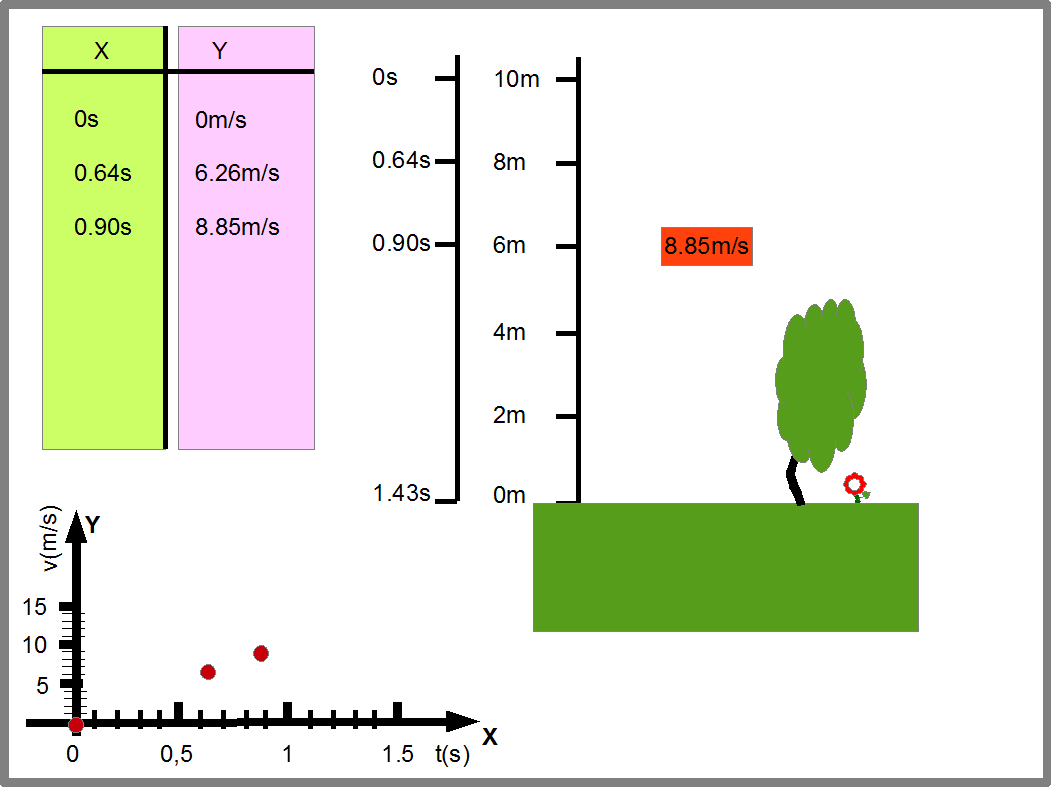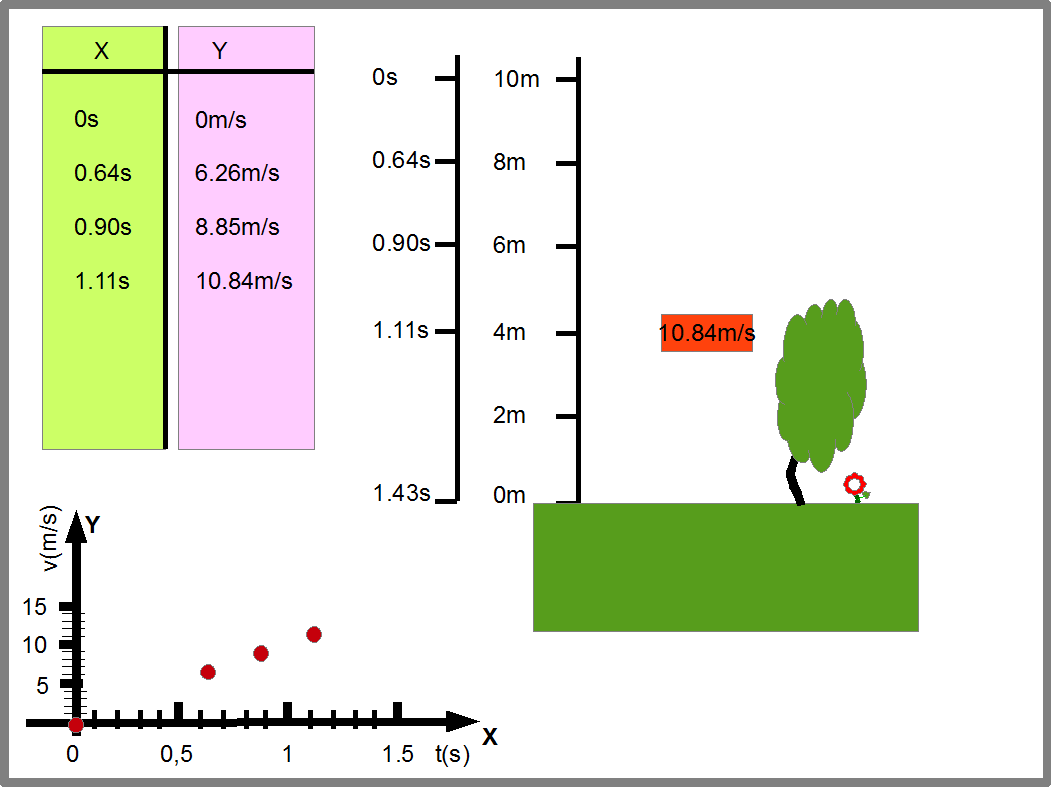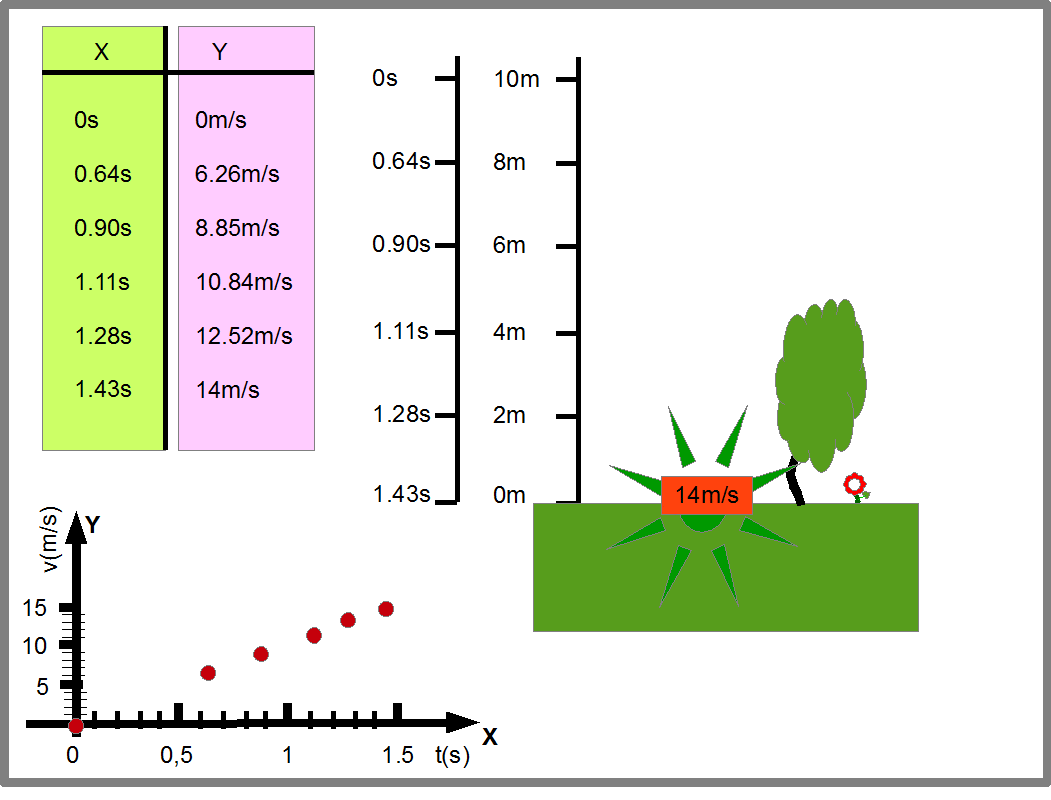
Рис.17
Если мы захотим узнать как при падении камня менялась его скорость от расстояния до Земли, то надо составить таблицу пар «расстояние до Земли-скорость камня» в разные моменты времени падения (Рис.18).

Рис.18
Во всех этих случаях мы определяли функции измеряя значения пар Х-Y, и записывая результаты или в виде таблиц, или графика. Эта таблица или график определяли искомую функцию Y=f(X) (Рис.19). В этом случае, сама функция и все значения функции определяются из эксперимента.
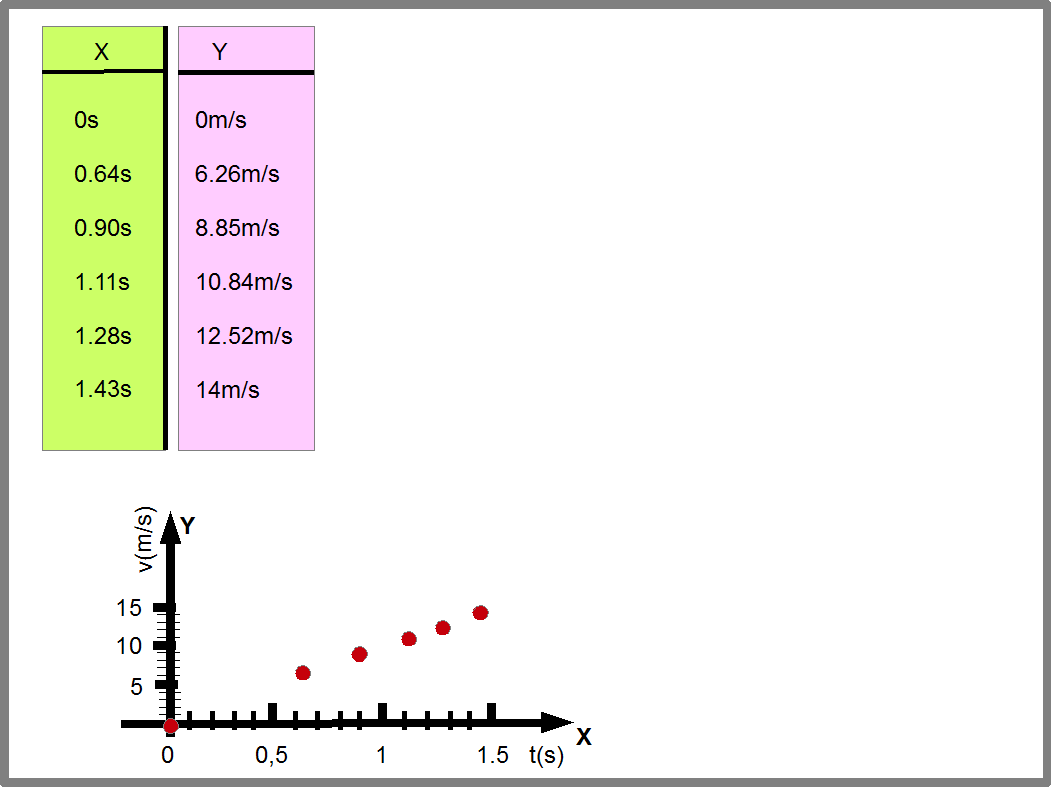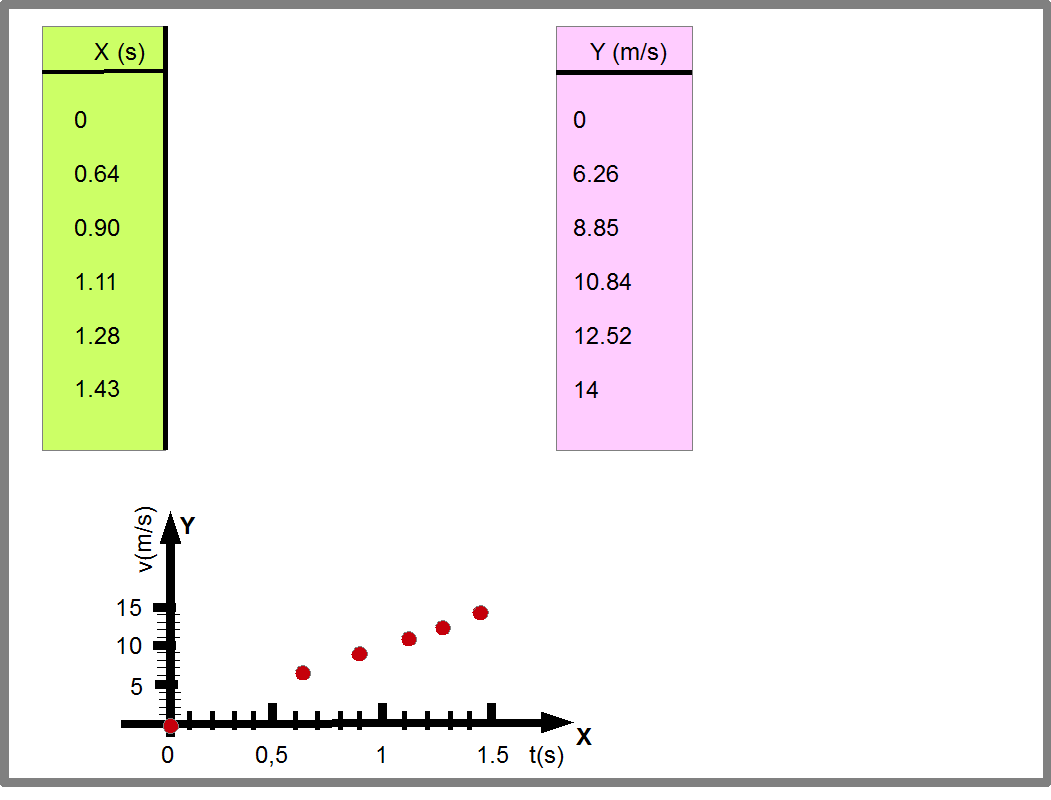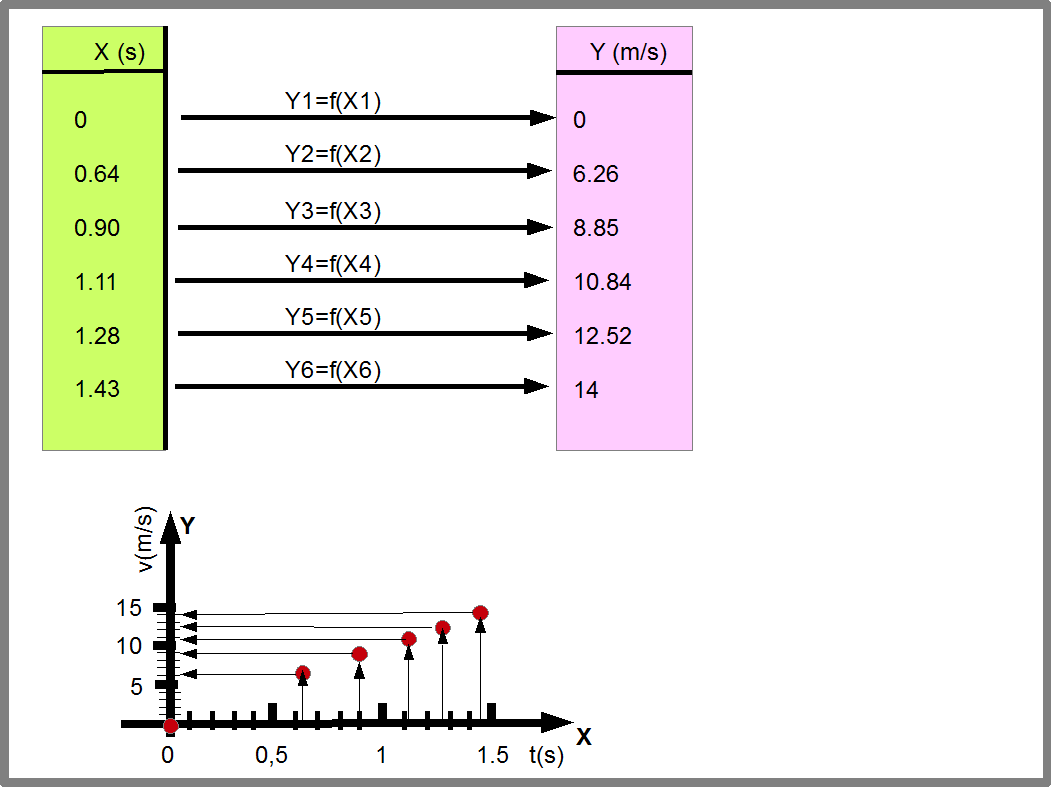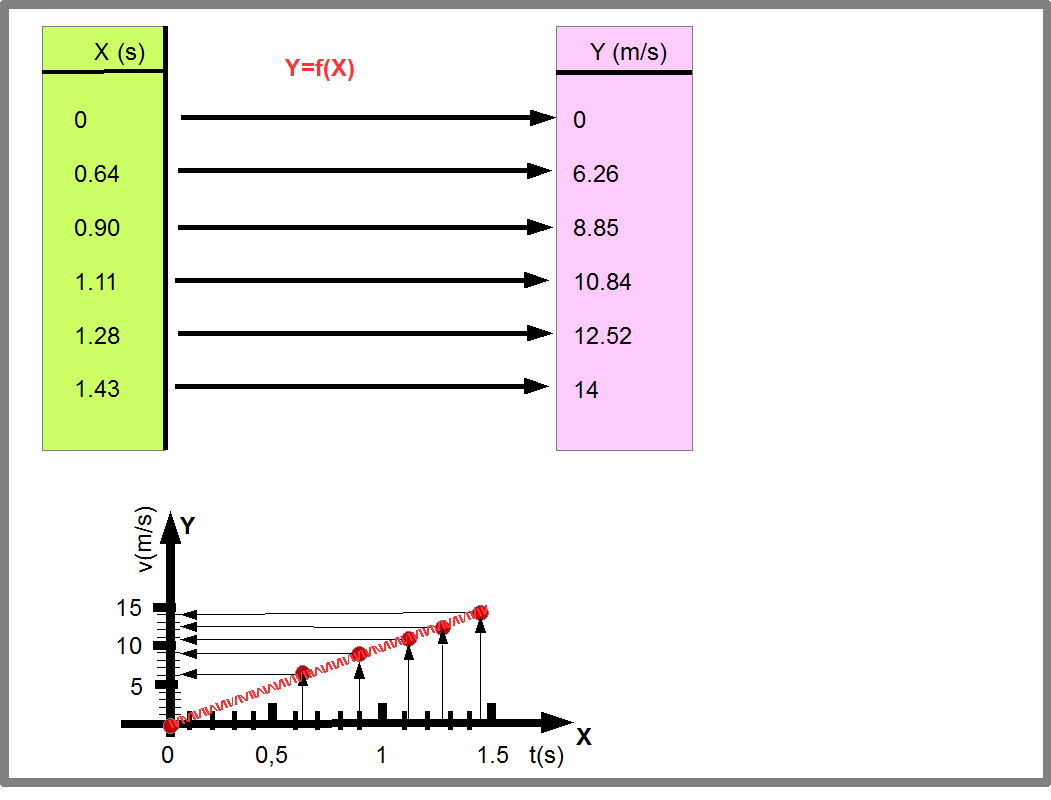
Рис.19. Рисунок показывает, как функция Y=f(X) задается с помощью таблицы и графика (на нем функция Y=f(X) показана красной линией). Обратите внимание, что функция Y=f(X) действует на каждую точку своей области определения, приводя ей в соответствие точку из области значений. Поэтому, функция определяется каждой парой точек X1Y1, X2Y2, X3Y3, X4Y4, X5Y5, и X6Y6. В простейшем случае, когда график Y=f(X) прямая линия, нам достаточно 2 точек, чтобы определить функцию. В более сложных случаях, чтобы точнее определить функцию требуется как можно больше точек.
Определив пары чисел X1Y1, X2Y2, X3Y3 ….. мы сможем сказать, какая была функция данного преобразования. Другими словами, мы определим функцию исследуемого преобразования. Т.е. назвав их,. Замерив эти пары экспериментально несколько раз, мы сможем сказать насколько стабильно наблюдаемое явление. Например, если область определения не меняется (т. е. X1, X2, X3.... не меняются), а значения Y в парах стали меняться, то значит меняется и функция. И наоборот, если функция меняется, то меняются и значения Y в этих парах.
Поэтому, задать такие пары чисел, это значит определить/задать функцию преобразования. Этим мы определим само наблюдаемое явление. Например, без понятия о функциях, нам было бы сложно точно рассказать кому-то или сохранить в памяти, как именно падал кирпич со второго этажа, Ведь нам бы пришлось говорить, как именно кирпич ускорялся, и какую именно скорость он достиг. Без использования чисел это сделать невозможно. Кроме того, кирпич мог бы быть сделан из разных материалов: цемента, пенопласта, дерева и полый внутри. В вакууме они бы падали одинаково. Но в воздухе их скорости падения будут разными из-за сопротивления со стороны воздуха. Описание явлений с помощью функций заданных таблицами распространен при анализе «больших данных» в микробиологии, в медицине или ядерной физике.
Например, когда надо найти эффективность вакцины, то проводят исследования большого количества, не менее 20 тысяч человек. Их делят на несколько групп в зависимости от возраста, состояния здоровья. Затем части из них делают прививку и сравнивают их заболеваемость с теми, кому прививку не делали. Полученные функции заболеваемости людей в зависимости от прививки и от хронических заболеваний определяют готовность вакцины к массовому применению.
Но в науке необходимо не только уметь измерять и находить закономерности из эксперимента. Надо еще уметь находить логику в закономерностях, определенных экспериментально. Надо искать Божественную логику создания материального мира. Надо уметь находить, как одни явления связаны с другими. Для этого надо уметь объяснять эти закономерности через закономерности обнаруженные ранее, находить в них то, что их объединяет, и то, что различает.
Например, после столетий исследований, человечество пришло к выводу, что в мире существует только 4 основных типа сил: электромагнитные, гравитационные, слабые ядерные силы, и сильные ядерные силы. Есть 4 основных состояния материи: газообразное, жидкое, твердое, плазма. К ним еще иногда добавляют Бозе-Эйнштейновский конденсат (например, сверхтекучая жидкость) и временные кристаллы (Рис.20). Понимание Высшей логики позволяет предсказывать явления, находить ошибки в измерениях, разрабатывать новые материалы и приборы.

Рис.20. Внутри этого квантового Google суперкомпьютера находится вычислительный чип, электромагнитный резонатор, состоящий из сверхпроводящих алюминиевых полосок по которым движется электрический заряд при температуре жидкого гелия (-269C, поэтому сам коомпьютер находится в гелиевом криостате, на фото он не показан). Колебания этого заряда могут происходить только при некоторых частотах. Эти электромагнитные колебания определяют квантовые состояния компьютера. Временной кристалл означает, что эти колебания чередуются в определенном порядке в течении относительно долгого времени не угасая при определенных температурах.
Поэтому необходимо во всем множестве природных явлений уметь видеть, как они сводятся к базовым понятиям. Для этого ученые придумывают различные модели явлений. Конечная цель таких моделей- смоделировать функции, которые бы совпадали с измеренными экспериментально и позволяли бы предсказывать результаты измерений. В таких случаях возникают ситуации, когда функция считается известной и известны исходные данные (область определения функции), а требуется найти значения функции (Рис.21).
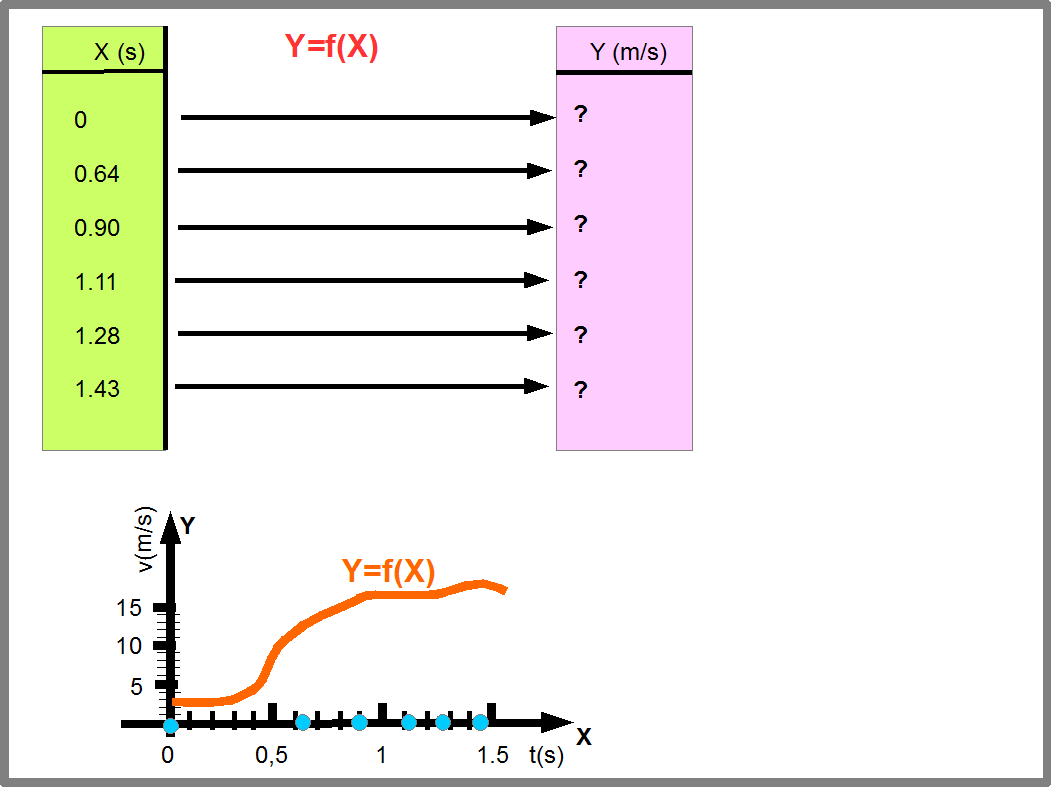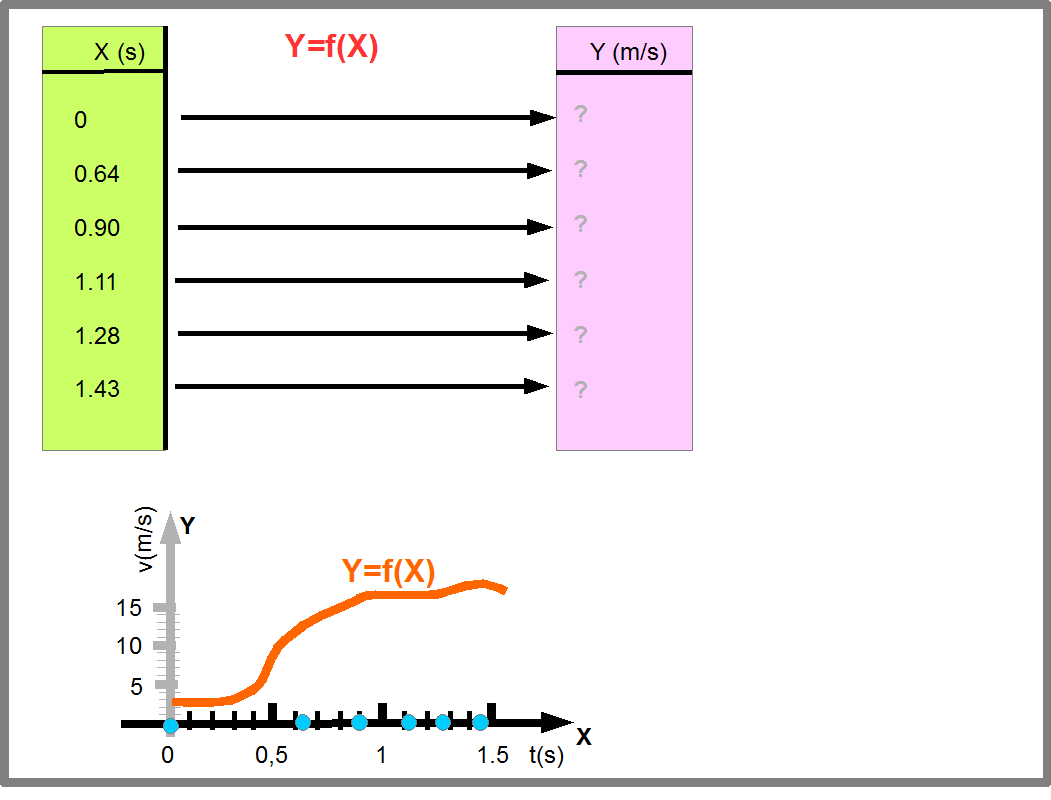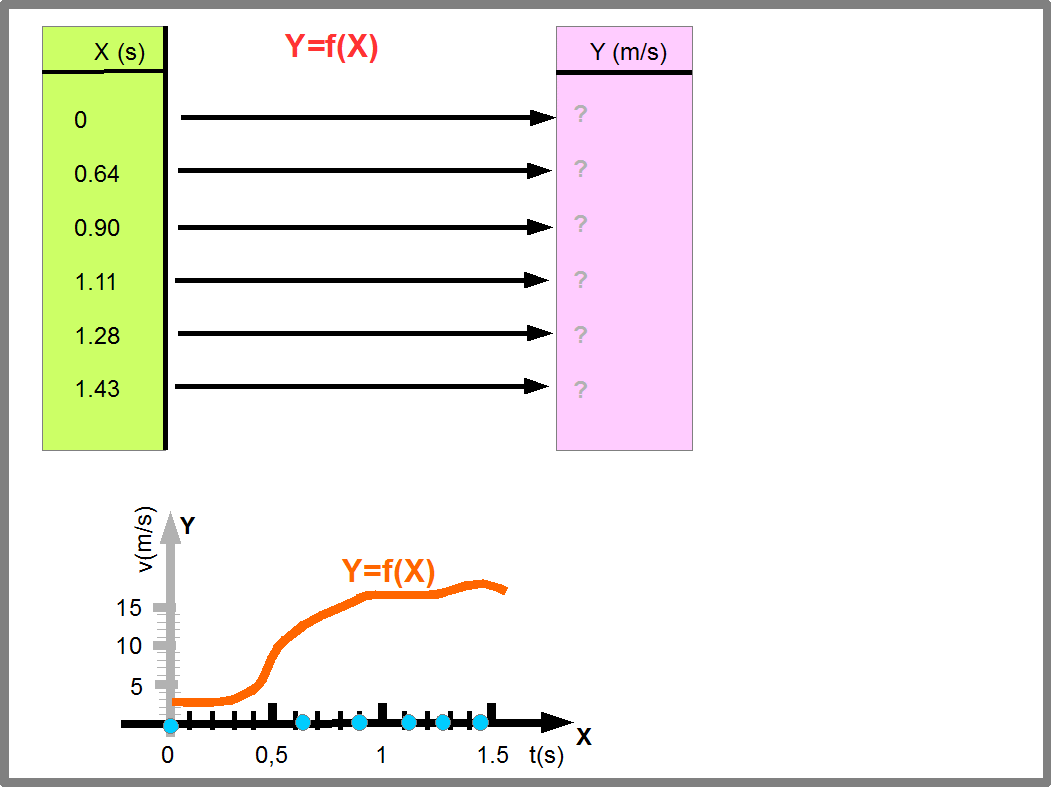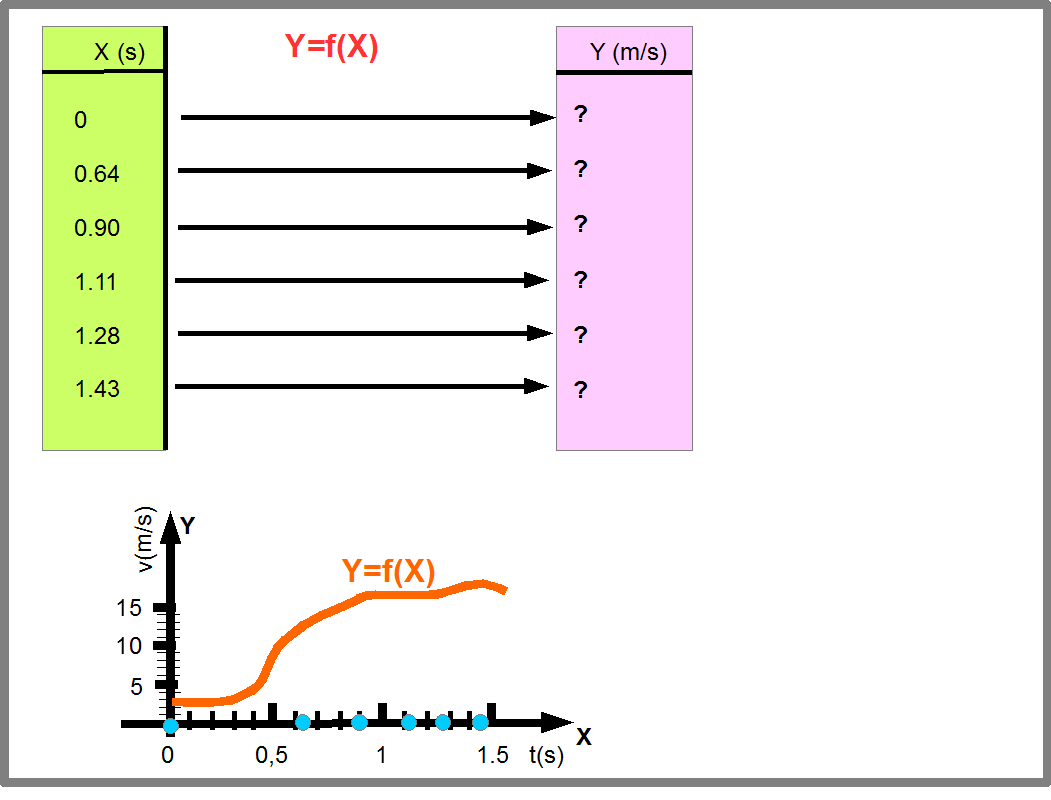
Рис.21
Как найти значения зависит от способа задания функции. Рисунок 22 показывает, как вычисляются значения функции Y=9.8*X, заданной аналитически, т.е. с помощью уравнения. Этим способом мы будем часто пользоваться в программировании.
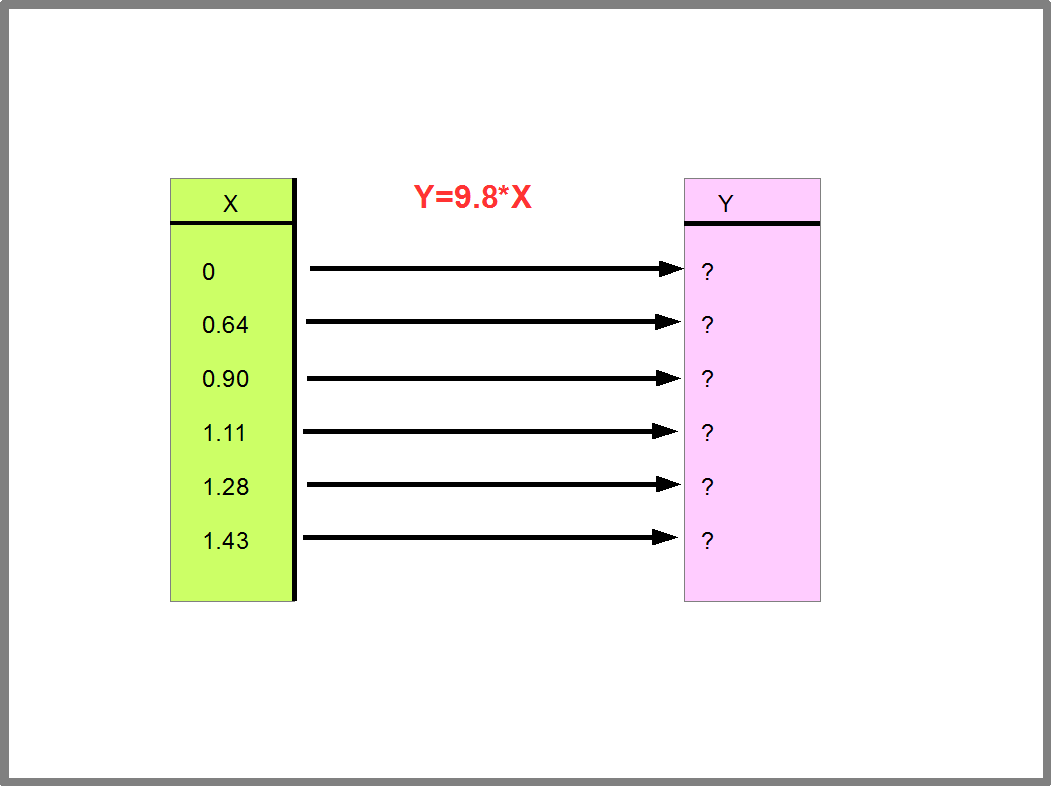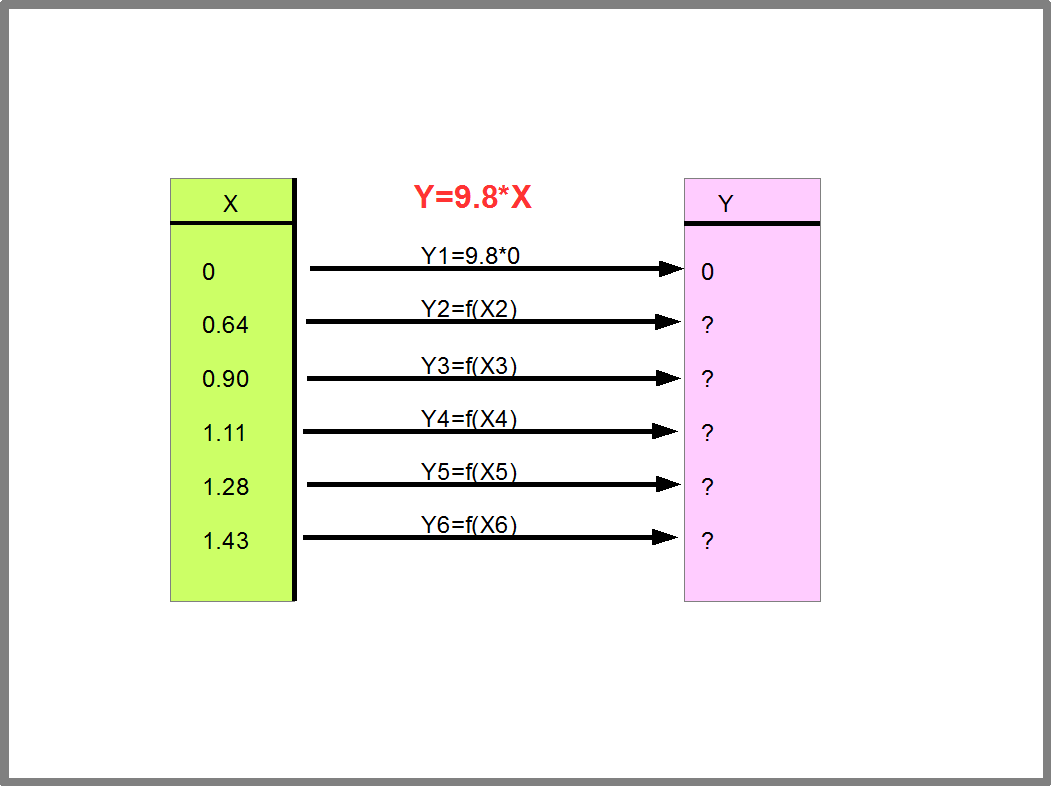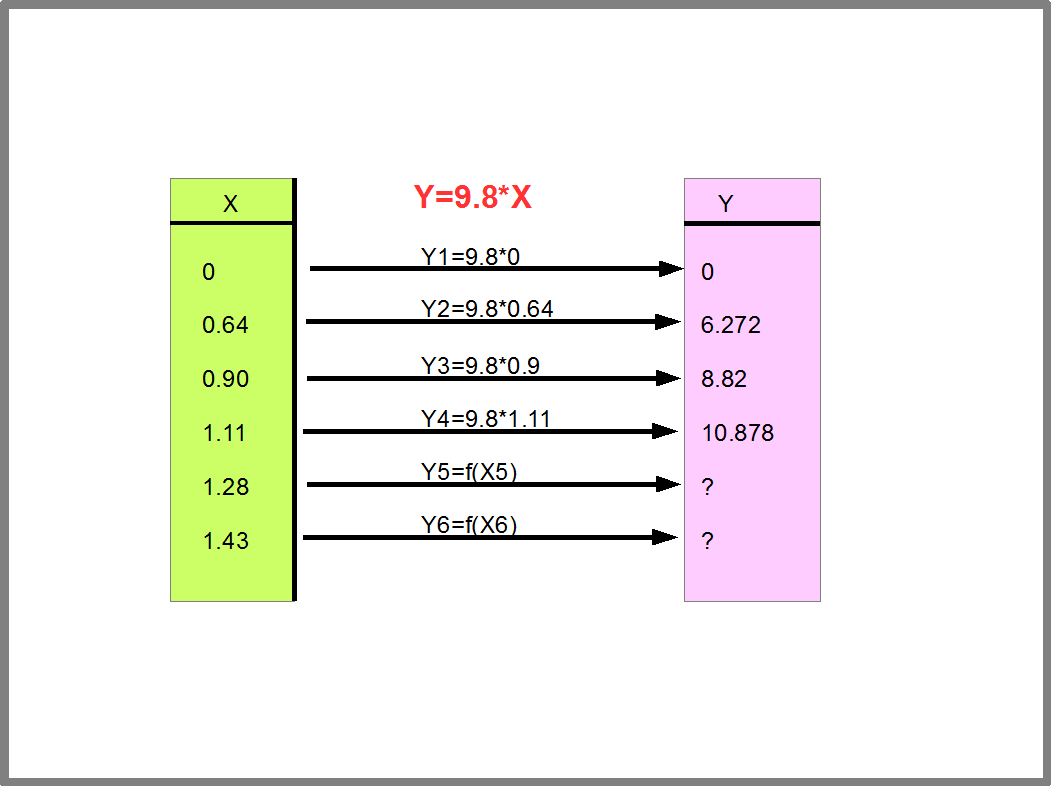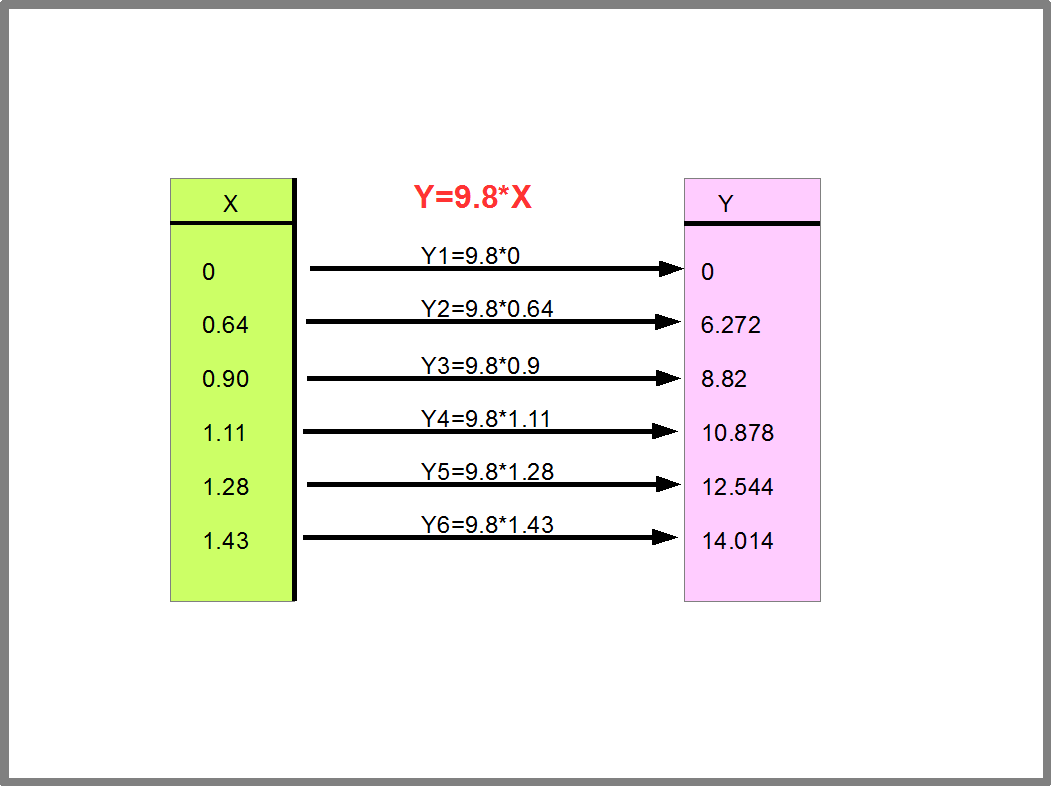
Рис.22. Вычисление значений функции Y=9.8*X.
Рисунок 23 показывает, как находятся значения функции заданной графически. Этот способ часто используется в инженерных расчетах.
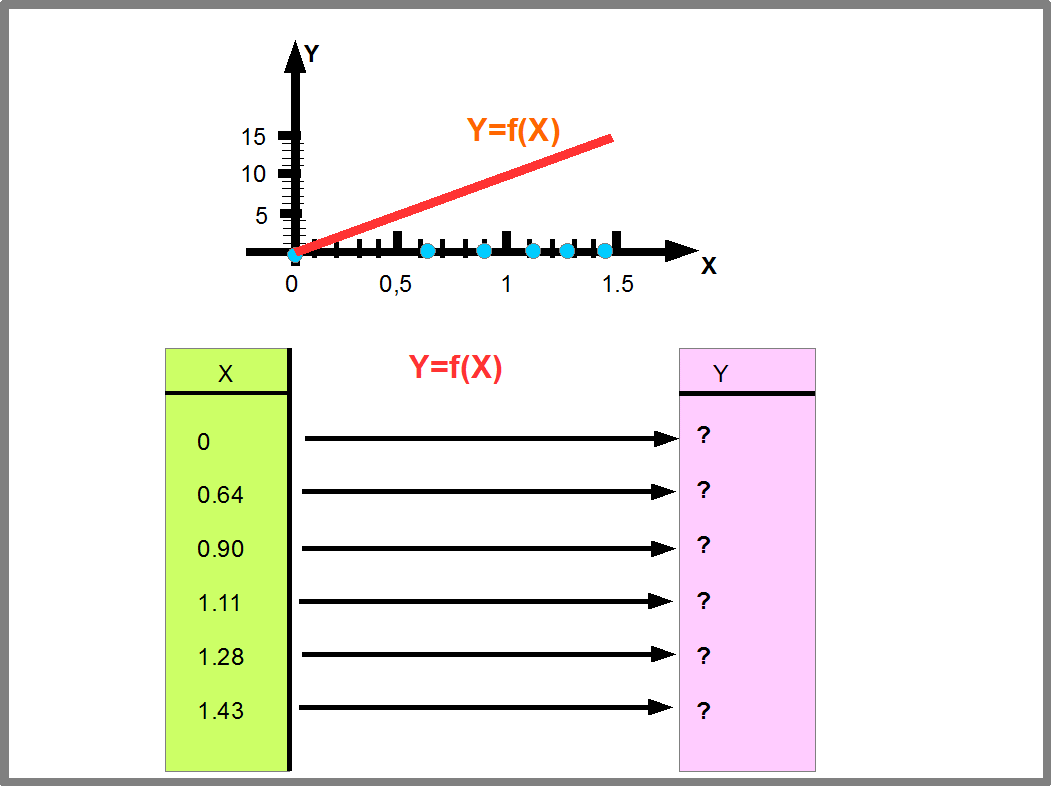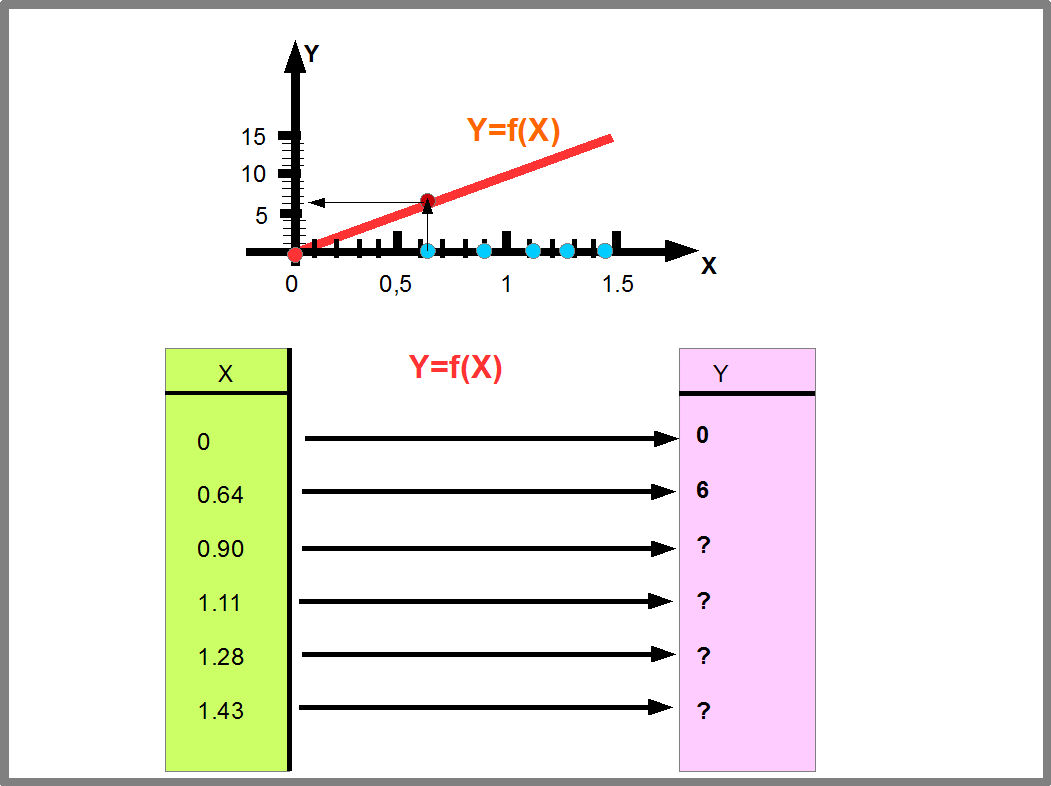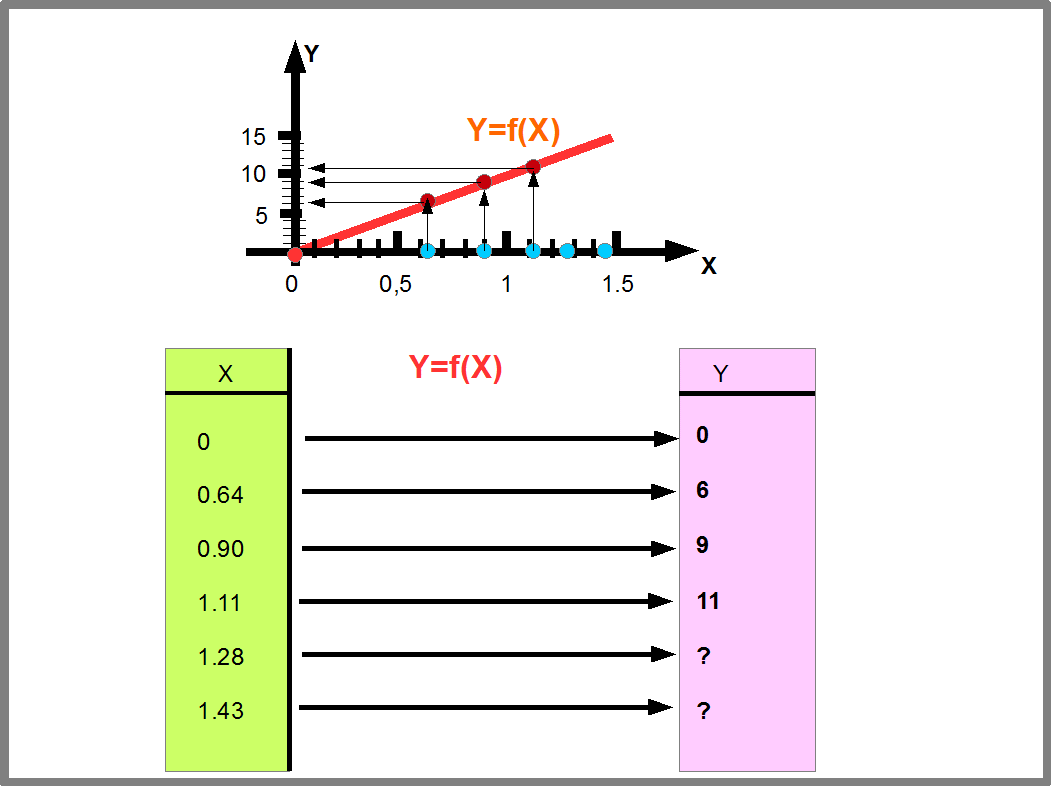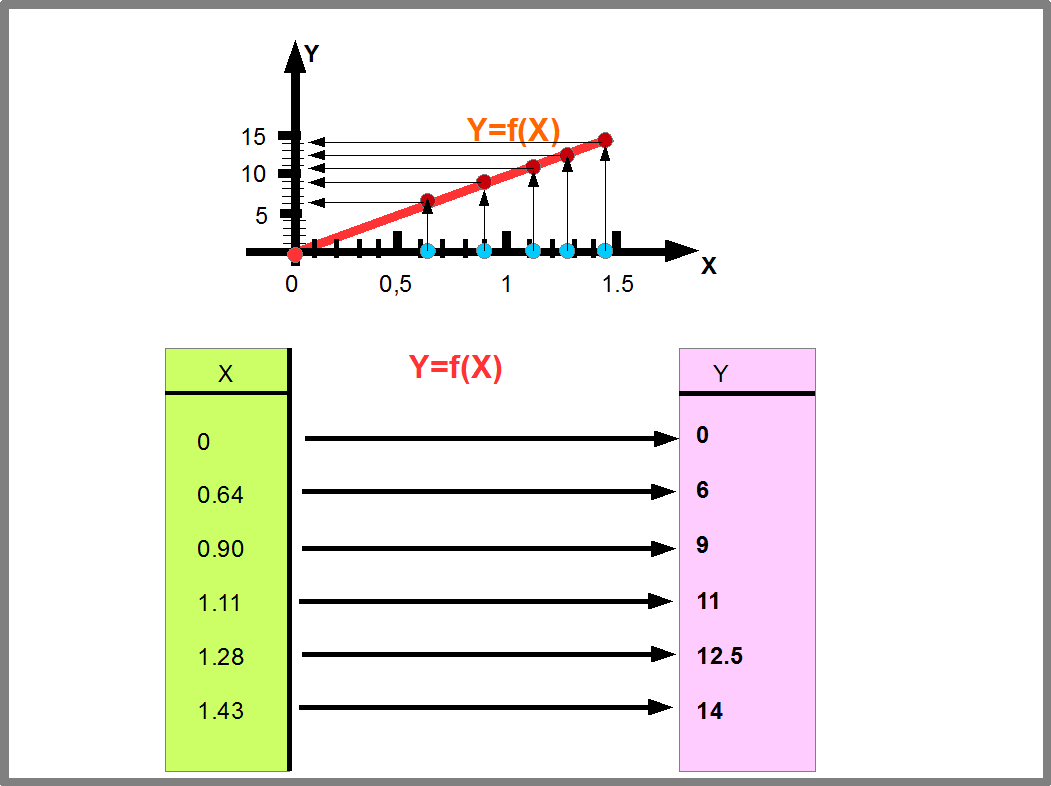
Рис.23
Существует только 5 различных способов определения/задания функции: с помощью 1) таблиц, 2) графика, 3) аналитического выражения (уравнения), 4) словесного описания, и 5) рекуррентного способа (когда есть многократно повторяемые преобразования, и каждое последующее преобразование определяется предыдущим. В таком случае областью определения может служить порядковый номер в последовательности преобразований) .
Для нас преобразование и функция очень важные понятия еще потому, что мы будем пользоваться ими для программирования и в таблицах OpenOffice.
В наших примерах, понятия "преобразование одного множества в другое" и понятие "функция" описывающая это преобразование, в общем-то, означают одно и то же действие преобразование, только разными способами. Поэтому они часто взаимозаменяемы. Но в математике, их могут различать. В математике, словом функция принято обозначать преобразования, когда область определения и область значений- это множества чисел. Если же преобразуются множество геометрических объектов в геометрические объекты, то это обычно принято называть преобразованием. Например, преобразованием будет, если область определения и область значений являются множеством векторов. Также в математике есть термин "преобразование функций". Например, пусть множество чисел, скажем множество А, было преобразовано в другое множество чисел В. Назовём это функцией f1. Для неё можно записать B=f1(A)). Пусть затем полученное множество чисел В было преобразовано в третье множество чисел С, назовем это преобразование f2. Для него можно написать C=f2(B). Тогда преобразование исходного множества чисел А в множество С- это тоже функция, назовем её f3, где C=f3(A). Функция f3 будет преобразованием функции f1. Однако, чаще преобразование функции называется функцией от функции. Для f3 можно записать: f3=f2(f1) или f3(A)=f2(f1(A)). Поскольку мы будем в основном работать с множествами чисел, то в дальнейшем мы будем чаще пользоваться термином функция. Более того, в физике преобразование векторов тоже обычно называется функцией. И под понятием функция будем понимать, как говорилось ранее, описание преобразования на языке математики одним из пяти перечисленных способов.
Практические задания по работе с графиками и таблицами.
Начнем мы изучение функций с задания их графиками и таблицами.
На прошлых занятиях вы играли в морской бой на клетчатой бумаге и знаете, что такое координаты. Рассмотрим клетчатое поле аналогичное полю морского боя, только для обозначения столбцов заменим буквы на цифры. То есть запишем цифры так же, как и для строк. Кроме этого, увеличим число клеток до 15. Тогда у нас горизонтальные и вертикальные координаты клеток будут целыми числами от 1 до 15. Горизонтальную координату будем называть осью Х, а вертикальную осью Y. Координатами, по прежнему будет пара чисел, которые мы будем записывать в скобках вот таким образом: (Х, Y), где вместо Х и Y мы будем записывать соответствующие значения координат клеток. Например, запись (3,5) означает точку на координатной плоскости, для которой координата Х равна 3, а координата Y равна 5. Обратите внимание, поскольку мы не используем теперь букв для координат, то чтобы не было путаницы, всегда первая цифра будет координатой Х, а вторая- координатой Y. Добавим еще точку с координатами (0,0). У нас получится такое поле (Рис.24), которое наывается координатной плоскостью.
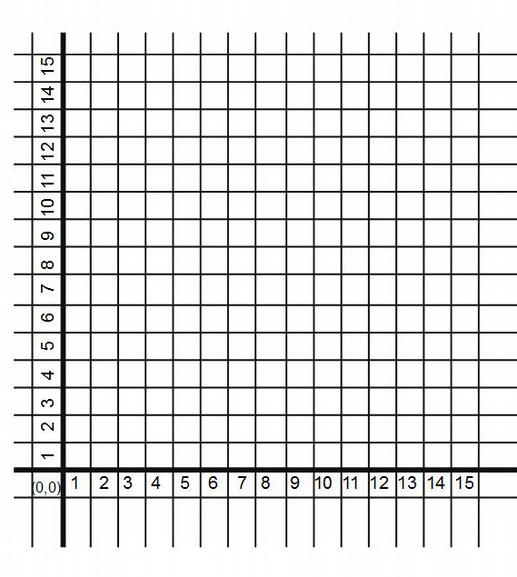
Рис.24. Поле с декартовами координатами
На этом поле проведем три разных линии (Рис.25):
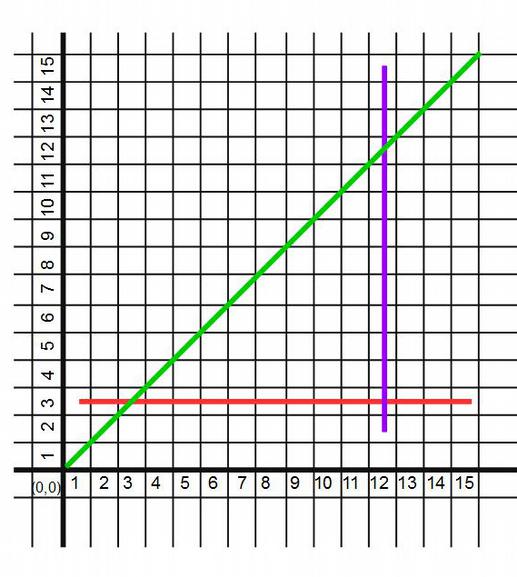
Рис.25. Три линии на координатной плоскости. Каждая из линий задаёт свою функцию, определяющую для каждой точки линии координату X и координату Y.
Обратите внимание, проведя линию мы задаём правило, по которому каждой точке оси Х можно поставить в соответствие определенную точку оси Y. Пусть например, точка по оси Х имеет координату 7. Тогда если мы возьмем зеленую линию, то точка линии с координатой Х равной 7 имеет координату Y равную тоже 7. А красная линия, аналогичным способом, поставит в соответствие точке Х равной 7 точку Y равную 3. Это означает, что зная линию, мы с её помощью всегда найдем для каждой её точки Х соответствующую точку Y. Таким образом, линия на координатной плоскости определяет функцию, ставящую в соответствие каждой точке оси Х, определенную точку оси Y. Т.е. мы задали правило преобразования точек множества Х в точки множества Y. Но конечно, это правило работает только для тех Х, для которых линия определена. Например, зеленая и красная линии определены для точек Х от 1 до 15, но не определены для точки X=0. А фиолетовая линия определена только для точки X=12. Как мы уже говорили, точки на которых определена линия (а соответственно и функция задаваемая линией) называются её областью определения.
Теперь мы оцифруем линии. Для этого представим, что мы играем в морской бой и нам надо точно попадать по линиям. Стрелять по точкам линий будем задавая их координаты так же, как мы стреляли по кораблям. Наши точные выстрелы будем записывать в виде таблицы с двумя колонками. В первой колонке, назовем её колонка Х, будем записывать Х координату точек. Во второй, в колонке Y, будем записывать соответствующую координату Y для каждой точки колонки Х. Например для зеленой линии получим следующую таблицу:
|
Х |
Y |
|
1 |
1 |
|
2 |
2 |
|
4 |
4 |
|
6 |
6 |
|
8 |
8 |
|
10 |
10 |
|
12 |
12 |
|
14 |
14 |
|
15 |
15 |
Вы конечно заметили, что я оцифровал не все точки, а только крайние и с четными Х. Можно было оцифровать все точки, а можно было было оцифровать и другие точки, например только с нечетным Х. Количество точек определяется только тем, насколько точно вы хотите задать вашу функцию. Минимальное количество точек, которые необходимо задать для прямой линии, равно 2 (почему??) . Максимальное число точек для зелёной линии в нашем случае будет равно 15, ведь мы используем для координат только целые числа. Но всегда желательно задавать крайние точки, поскольку они определяют области определения и области значений функции.
Для фиолетовой линии таблица может быть такой:
|
Х |
Y |
|
12 |
2 |
|
12 |
3 |
|
12 |
5 |
|
12 |
8 |
|
12 |
12 |
|
12 |
15 |
Домашнее задание 2. Пятая неделя
Задача 1.
а) eDrawings. Линейные преобразование параллельных прямых. Используйте присланный вам файл с двумя параллельными струнами, eDrawings и определите все возможные типы проекций параллельных струн на плоскость экрана. При работе используйте ортогональную проекцию, а струны вращайте всеми возможными способами.
б) Сделайте сами макет параллельных прямых из подручных материалов, и получите линейные преобразования параллельных прямых с помощью изменения угла наклона плоскости проецирования при параллельном проецировании. В качестве источника света для такого проектора используйте солнце или далеко стоящую лампу.
в) Линейные преобразование плоских фигур: круга, прямоугольника, параллелограмма, треугольника с помощью eDrawings и присланных вам файлов с геометрическими плоскими фигурами. Кто получит больше разных типов треугольников, четырехугольников, овалов в результате преобразований.
Задача 2.
Загрузите OpenOffice и просмотрите учебные фильмы, перечисленные ниже. Выполните/повторите все упражнения, которые делаются в учебных фильмах.
IV. Введение в программирование.
В данном курсе, для построения графиков и решения физических задач нам также потребуется некоторое программное обеспечение. Мы начнем с использования свободно распространяемого программного обеспечения LibreOffice (последнюю версию можно бесплатно загрузить здесь: https://www.libreoffice.org/download/download-libreoffice/). OpenOffice аналог этой программы (здесь можно бесплатно загрузить последнюю версию http://download.openoffice.org/ ). Но к сожалению, OpenOffice не поддерживается в рабочем состоянии и лучше использовать LibreOffice. Для этого укажите вашу операционную систему и загрузите LibreOffice (кликнете на Download). Программа закачает установочный файл на ваш компьютер. Это займет некоторое время. Потом запустите исполнительную программу кликнув на сохраненный файл. Дальше следуйте установочным инструкциям. Запаситесь терпением: инсталляция программы может занять до получаса.
Если у вас Windows10 или более новая версия, то вам потребуется установить Java Runtime Environment (JRE), 8-ю версию. Например, файл jre-8u361-windows-x64.exe или более новый. Здесь вы можете найти нужную вам версию: https://www.java.com/en/download/windows_manual.jsp а здесь краткое описание, как правильно выбрать версию и установить её: https://wiki.documentfoundation.org/Faq/General/InstallJava. В некоторых случаях вам потребуется установить еще Visual C++ Redistributable Package : VC_redist.x64.exe, который можно скачать вот отсюда https://learn.microsoft.com/en-us/cpp/windows/latest-supported-vc-redist?view=msvc-170.
Внимание тем, у кого операционная система Linux!!!
Вам загружать LibreOffice не надо. У вас он есть по умолчанию. Если вы хотите установить Linux на вашем компьютере, то рекомендую успользовать Ubuntu. Здесь подробная инструкция, как установить Ubuntu: https://ubuntu.com/tutorials/install-ubuntu-desktop#1-overview.
После установки LibreOffice, Вам надо открыть LibreOffice Math (OpenOffice Calc для техт у кого OpenOffice).
Здесь учебные фильмы, которые объяснят как пользоваться таблицами Spreadsheets в OpenOffice Calc/LibreOffice Math:
Введение. Использование таблиц в качестве калькулятора: https://youtu.be/GPvK7brpOzo
Введение. Функции и графики:
Работа с графиками. Делаем таблицу умножения:
Основная информация содержится в учебных видео, но на всякий случай ниже приводятся текстовые пояснения, как начать работать с таблицами в OpenOffice Spreadsheets:
Задача 3.
а) Возьмите клетчатую бумагу. Используя таблицы оцифровок к Рис.25, и постройте по ним графики линий.
б) Проведите оцифровку окружности (рисунок 26) и постройте по полученным данным график в OpenOffice Spreadsheets. Какую разницу между рисунком 26 и вашим графиком вы обнаружили? Как вы думаете в чём причина этой разницы?
Если у вас возникли проблемы с построением графиков, то воспользуйтесь учебным видео: https://youtu.be/HgsfXzyRwSg.
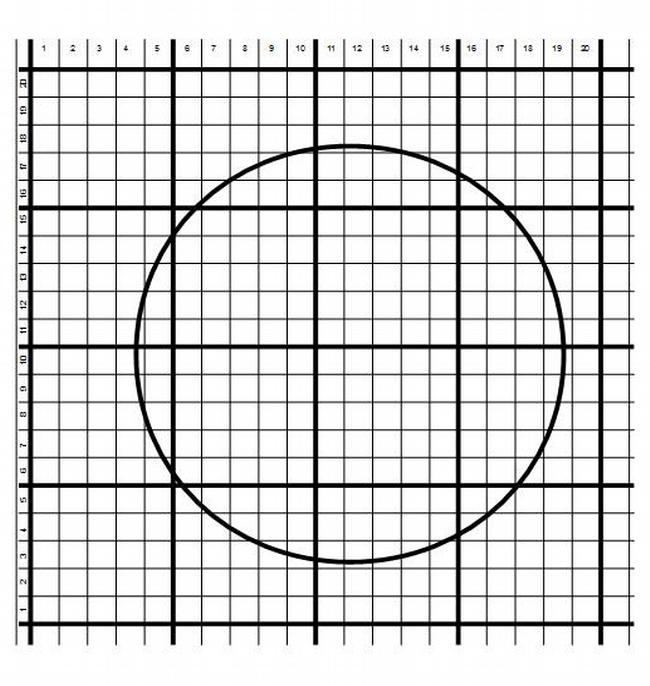
Рис.26
Ниже приводится текстовые пояснения, как начать работать с таблицами в OpenOffice Spreadsheets.
После того, как соответствующая программа будет открыта, Вы увидете таблицу (Рис.27а).
Сама таблица напоминает поле игры «Морской бой». Как и в морском бое, каждая клетка таблицы имеет координату, например А1 или C5. Но поле таблицы конечно много интереснее. Причина тому, оно по сути своей очень близко к памяти компьютера, которая тоже имеет двумерные кооординаты своих ячеек памяти. Также как и в памяти компьютера, в ячейках таблицы может сохраняться различная информация. Её можно посмотреть наведя курсор на соответствующую ячейку и кликнув левой кнопкой мышки. Содержимое ячейки появиться в поле обведенном фиолетовой кривой на Рис.27.а. И обратно, если мы выделим ячейку и запишем в этом поле что-то, а затем нажмем на Enter, то записанное сохранится в выделенной ранее ячейке.
Что можно сохранить в ячейке таблицы? Числа, текст и функции. Таблица сама отличает десятичные числа от текста и от функций.
Различает по простому принципу: то что состоит из цифр- это число. То что состоит из букв или любых знаков, но при этом первый знак ' (например, abc или '123)- относится к string, т.е. текстовой информации.
Если первым стоит знак равенства =, то это табличная функция (например, =sum(A1:D1) означает функцию суммирующую числа стоящие в ячейках от А1 до D1: A1, B1, C1, и D1).
Так же как и в памяти компьютера, в таблицах практически реализованы два типа адресации: прямая и косвенная. При прямой адресации, мы находим или сохраняем данные в ячейке с указанным адресом.
Например, можем сохранить в ячейке А1 число 7. Для этого наведите мышкой курсор на ячейку А1 и напечатайте цифру 7. Потом нажмите на клавишу Enter, чтобы сохранить цифру в ячейке. Если теперь опять навести курсор на ячейку с цифрой 7, то и в поле значений Вы увидете ту же «7» (поле значений обведено фиолетовым элипсом на Рис.27.а.). Это же поле значений используйте для редактирования/исправлений содержимого ячейки. Последовательность действий при редактировании обычная. Сначала выделяете мышкой с помощью курсора нажав при этом на левую клавишу мышки то, что хотите исправить. Затем печатаете исправления. Того же эффекта можно достичь выделяя с помощью стрелок и одновременного нажатия клавиши Shift на клавиатуре.
В случае косвенной адресации, по указанному адресу будут находится не данные или команда, а адрес ячейки, где находятся данные. Например, если мы запишем в ячейку В3 таблицы следующую «табличную» функцию (не забудьте нажать на клавишу Enter после того, как впечатали формулу):
= A1
приравнивающую значение ячейки В3 значению ячейки А1, то ячейка В3 будет содержать адрес другой ячейки А1, где и находятся реальные данные. При этом в ячейке В3 мы увидим число 7, но в поле значений будет =A1 (Рис.27.б).
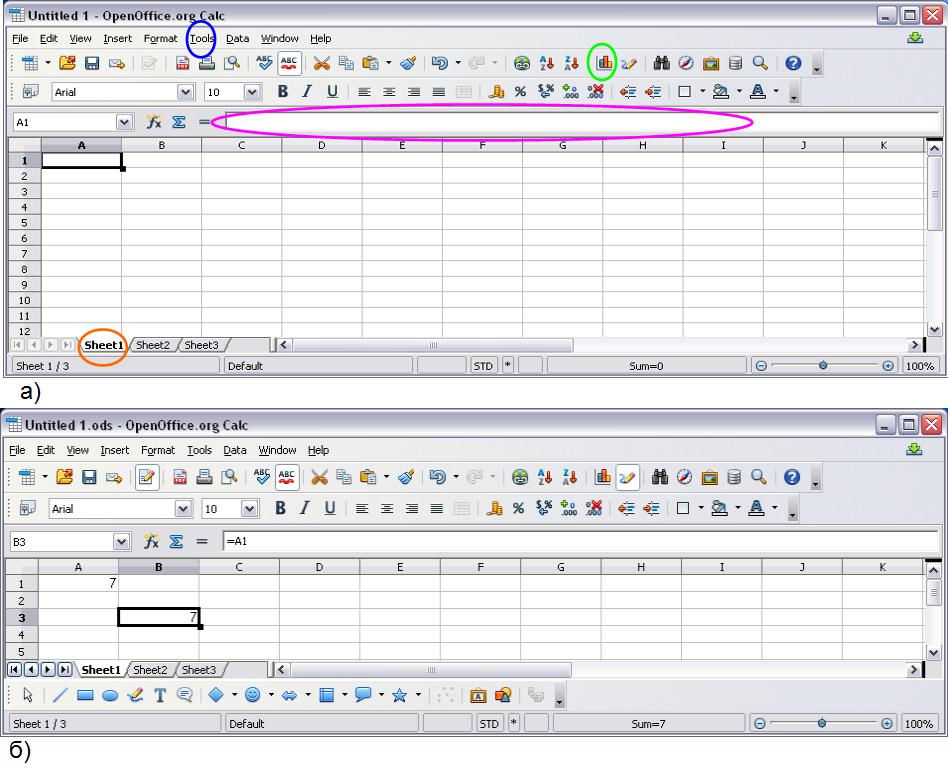
Рис.27. а) Вид открытого листа OpenOffice таблицы. Обратите внимание таблицы содержат 3 листа. Открыт первый (обведено оранжевой линией). Название листа Sheet1 можно отредоктировать кликнув два раза на него и вписав желаемое имя в появившемся окне; б) запись и чтение данных в ячейках таблицы. В обоих случаях сначала надо навести курсор на требуемую клетку таблицы. Затем кликнуть левой клавишей мышки. Этим Вы выделите клетку и вокруг неё появится утолщенная черная рамка. Например, на рисунке выделена клетка В3. При этом значение клетки равно 7, а в поле значений видно, что в клетке записана функция =A1 , приравнивающая её значение к значению клетки А1. Содержимое клетки можно изменить. Для этого можно либо просто напечатать её новое содержание, которое автоматически будет вписано в выделенную клетку; либо навести курсор на поле значений и кликнуть левой клавишей мышки, а затем выполнить необходимые исправления. Если в этот момент Вы передумали исправлять, то можно нажать на клавиатуре кнопку Esc. Этим Вы диактивируете клетку. После выполненных исправлений нажмите кнопку Enter, чтобы исправления в клетке сохранились.
Адресация в таблицах имеет еще одно интересное свойство. Запишите в ачейку C5 функцию =G5, и нажмите Enter. Теперь наведите мышку на ячейку А1 и щелкните левой клавишей мышки. Вокруг ячейки появиться черная рамочка. Это вы активировали ячейку. Теперь не нажимая на клавиши, наведите мышку на нижний правый угол ячейки C5так, чтобы появился крестик. Затем нажмите левую клавишу и, продолжая ее держать, сдвиньте мышку на соседнюю нижнюю ячейку C6. Отнустите клавишу. В ячейке C6 появиться некоторое число или сообщение. Наведите мышку на ячейку C6 снова и щелкните левой клавишей. Вы увидите значение ячейки C6. Это будет =G6. Т.е. таким образом вы скопировали функцию ячейки C5 в ячейку C6, но при этом область определения функции поменялась, тоже на одну клетку таблицы. Чтобы при копировании функции сохранялась ее область определения, нужно было записывать адреса в исходном уравнении следующим образом: =$G$5.
Теперь запишите в С5 функцию =G5, и скопируйте ее в ячейки В5, D5, и С4. Посмотрите что у вас получилось в тих случаях.
Повторите тоже самое для фунции =$G$5.
Поэкспериментируйте сами с этой записью и посмотрите, что получится, если вы запишите и будете копировать следующие функции
а) =$G5
б) =G$5
Ниже приводится список других часто употребляемых табличных функций:
=power(a;b) - означает выражение ab, например =power(2;3) даст 23 =2*2*2=8; = power(8;1/3) даст 81/3=2 . Функция = power(8;1/3) является обратной функции =power(2;3), на что указывает второе число в скобках. Обратите внимание, что в Excel таблицах компании Microsoft числа разделяются просто запятой вместо точки с запятой. Например, в Excel надо писать: =power(2,3) . Задание значений a и b возможно с использованием косвенной адресации. Например : =power(E3;F1) возведет число по адресу E3 в степень числа, находящегося по адресу F1.
У этой функции есть две перменных. Первая переменная (первое число в скобках) называется основанием степени. Вторая переменная- второе число в скобках- показатель степени, в которую возводится основание степени. Обычно они применяются так, что одна из переменных фиксирована, и не меняется. Тогда фиксированная переменная называется параметром.
Если зафиксирован показатель степени b, то функция =power(a;b) называется степенной функцией. Ее областью определения, переменной а, могут быть любые числа если b>0 или b=0; итолько положительные числа, если b<0.
Если зафиксировано первое число, основание степени а, то функция называется показательной, или ее иногда называют экспоненциальной функцией. Тогда, областью определния функции, переменной b, могут быть любые числа, если a целое число; и только положительные числа, если b дробное число.
= sqrt(a) – означает квадратный корень числа а. Например =sqrt(4) даст 2. Как обычно, можно использовать косвенную адресацию.
-Чтобы подсчитать произведение величин сохраненных в ячейках, надо записать через произведение адресов ячеек. Например, запись = A2*D3 подсчитает произведение данных в ячейках A2 и D3. Аналогично можно найти результат деления, сложения или вычитания: = A2/D3 ; = A2+D3; = A2-D3. Если же у Вас есть числа которые просто надо сложить, например Вам надо сложить 23 и 45, то это можно сделать записав =23 + 45. Но обычно лучше сначала данные сохранить в ячейках, а затем оперировать ячейками используя косвенную адресацию.
=max (a:b) – находит максимальное значение в ячейках с адресами с а по b. Например, =max(C3:C5) находит максимальное значение в ячейках с C3 по C5 : C3, C4, C5 .
Аналогично работает нахождение минимума . Наприемр, =min(C3:C5) найдет минимальное значение по тем же адресам.
= pi() - вернёт значение числа . Обратите внимание на скобки: они пустые. Это просто константа, постоянное число, которое в программировании так обозначается. Его не записывают просто числом, потому что никто не знает абсолютно точной записи этого числа, хотя это число существует, и на числовой прямой можно найти точку, у которой координата равна абсолютно точно числу . Его значение всегда приводится округленно, с точностью, которая вам нужна и которую может вычислить компьютер.
=exp(a) - находит значение экспоненты числа а или если а это адрес, то экспоненты числа стоящего по адресу а. Например: =exp(2) даст 7.39. Область определения функции, переменная а, любое число. Функция является частным случаем функции =power(a;b), при а=e. Число е аналогично числу . Оно тоже существует, но его абсолютного точного сначения тоже никто не знает. Как и в предыдущих случаях, вместо прямой адресации можно использовать косвенную адресацию, т.е. вместо числа можно использовать адрес ячейки, где находится число.
=log(number; base) –вычисляет значение логарифма числа number по основанию base. Например, =log(100;10) даст два. Вместо чисел можно использовать адреса ячеек, где находятся числа. base-основание логарифма, любое положительное число, больше нуля. Это параметер функции, т.е. основание выбирается и после этого, обычно, не меняется. Область определения функции, переменная number, любое положительное число.
Функция авляется обратной функции =power(a;b).
=ln(number) –найдет значение натурального логарифма числа number. Функция является частным случаем функции =log(number; base), при base=e. Число е аналогично числу . Оно тоже существует, но его абсолютного точного сначения никто не знает. Как обычно, вместо прямой адресации можно использовать косвенную адресацию, т.е. вместо числа можно использовать адрес ячейки, где находится число.
Функция авляется обратной функции =exp(a).
=sin (b)
=cos(b)
=tan(b) - тригонометрические функции синуса, косинуса и тангенса. sin(b) и cos(b) измеряют проекции точек окружности с радиусом равном 1 на оси Yи X. При этом положение точек на окружности задается полярным углом b (см. игру Морской Бой в полярных координата). Функция tan(b) равна sin(b)/cos(b). Переменная b является углом измеренным в радианах. Областью определения функций, переменной b, могут быть любые числа. Как всегда, b либо само число, либо адрес числа.
=аsin (a)
=аcos(a)
=аtan(a) - тригонометрические функции арксинуса, аркосинуса и арктангенса. Oбластью определения функций, переменной а, для функций =аsin (a) и =аcos (a) могут быть любые числа от -1 до 1 включая сами -1 и 1. Oбластью определения функции =аtan (a), переменной а, могут быть любые числа. Как обычно, a либо само число, либо адрес числа. Областью значений функций будут величины углов измеренных в радианах. Эти функции обратные функциям sin(b), cos(b), tan(b).
=DEGREES(b)
=RADIANS(b) - функции переводят радианы в углы и наоборот углы в радианы.Область определения функций- любые числа.
в) Введите таблицы оцифровок линий изображенных на рисунке 25, и постройте их график в OpenOffice Spreadsheets.
Задача 4.
Запишите числа в ячейки A2 и B2, как показано на рисунке 28. Обратите внимание, что Y должно получатъся из X с помощью преобразования Y=3*X+2. Поэтому в ячейку B2 записывается функция =3*A2+2. Постройте график Y от X для этой пары чисел X-Y.
Если у вас возникли проблемы с построением графиков, то воспользуйтесь учебным видео: https://youtu.be/HgsfXzyRwSg.
Что вы получили на графике?
Задача 5.
a) В колонку D запишите числа от 0 до 70 с шагом 0.2 , как показано на рисунке 28 (т. е. Вам надо скопировать одновременно две ячейки D2 и D3 до строки 352). Это будет область определения Х для последующих функций данной задачи.
В колонку E запишите значения Y с помощью функции Y=3*X. Сначала найдите значение Y для точки X=0 с помощью функции Y=3*X. Для этого в ячейку E2 запишите функцию =3*D2, аналогично тому, как вы делали это в предыдущей задаче. Затем скопируйте эту ячейку до строки 352, как показано на рисунке 28.
Таким же способом заполните область значения функции G=Y/3 в колонке F. Будьте внимательны: G является функцией от Y. Поэтому, колонка E содержит область определения функции G. В этом случае, например, в ячейку F2 надо записать функцию =E2/3, а затем скопировать ее в остальные ячейки колонки F до 352 строки (см. Рис.28). Сравните полученные значения функции G (значения ячеек колонки F) с значениями переменной X из колонки D. Почему они одинаковые?
В итоге мы получили преобразования X->Y->G. Или другими словами, получили функцию G от функции Y, которая в свою очередь есть функция от X. Поэтому, функцию G можно записать так: G(Y(X)).
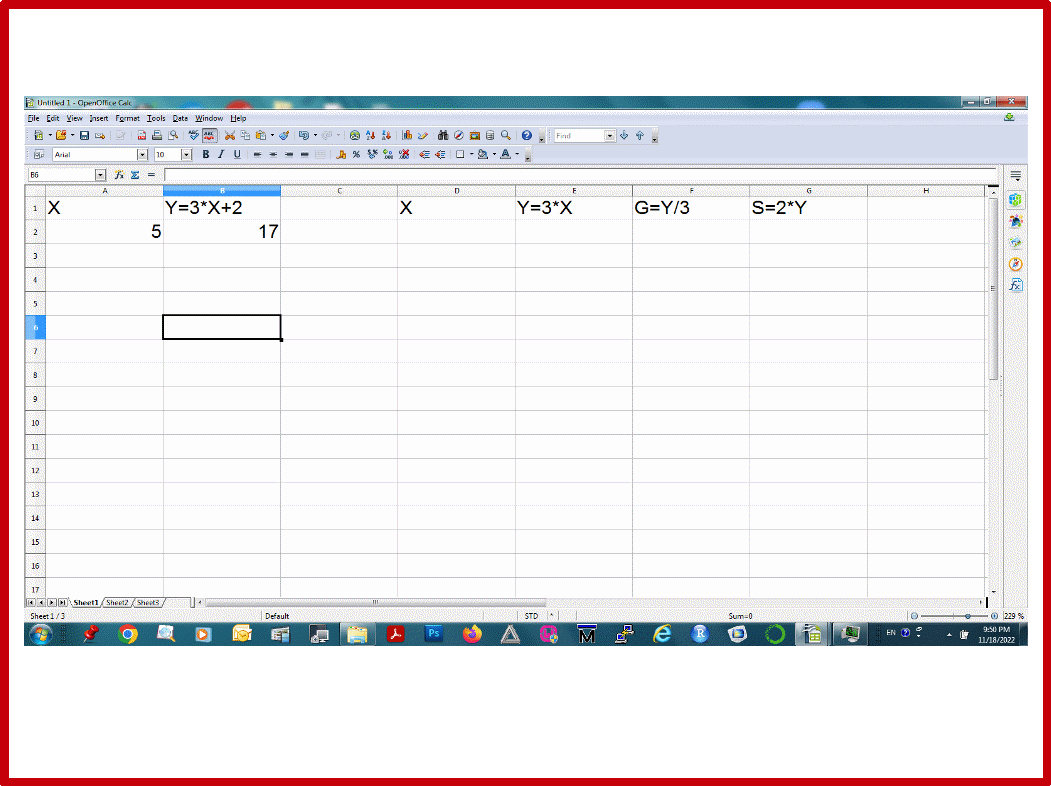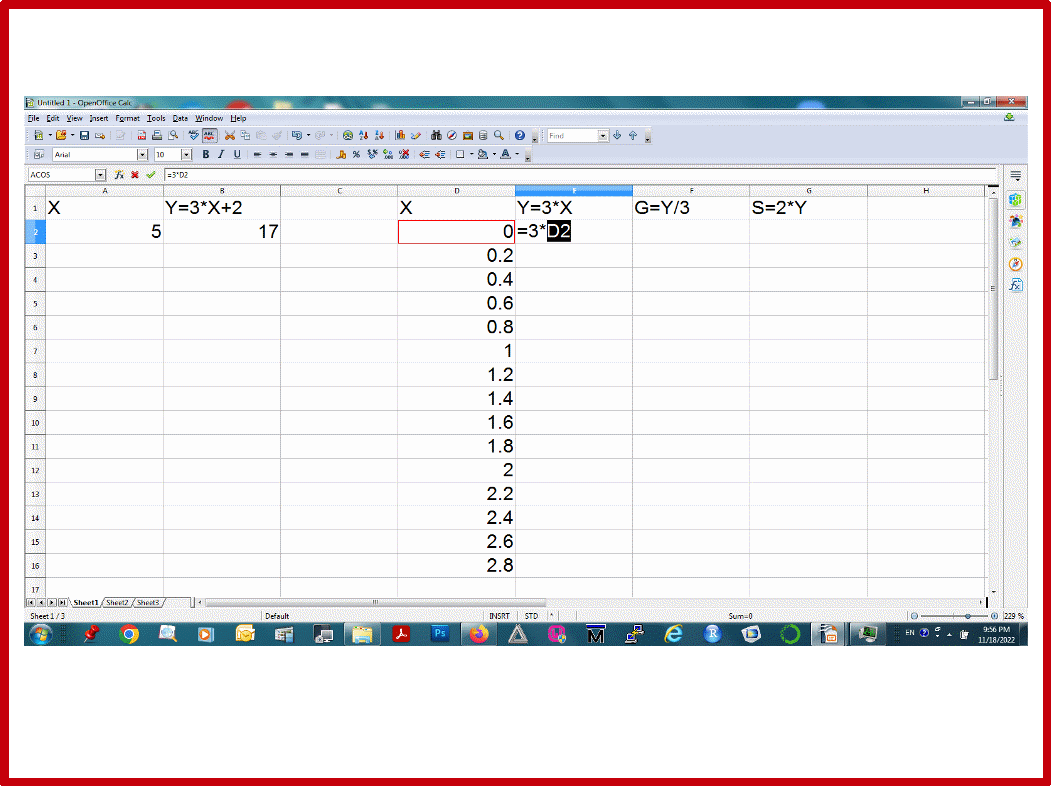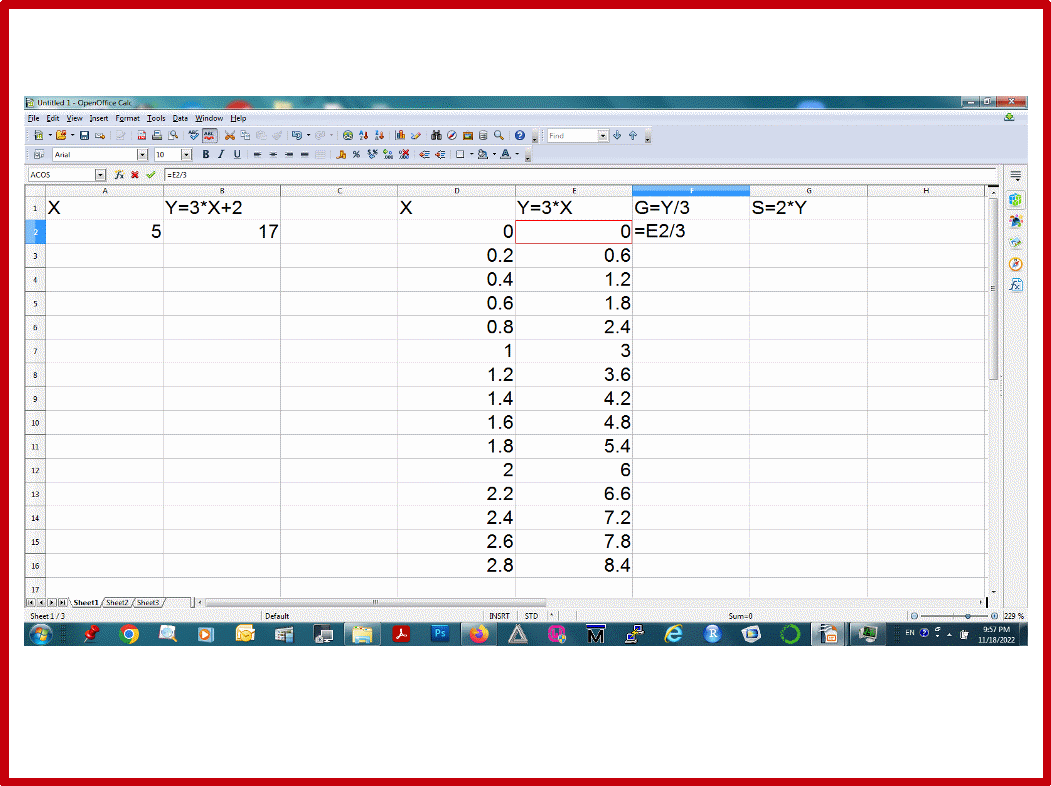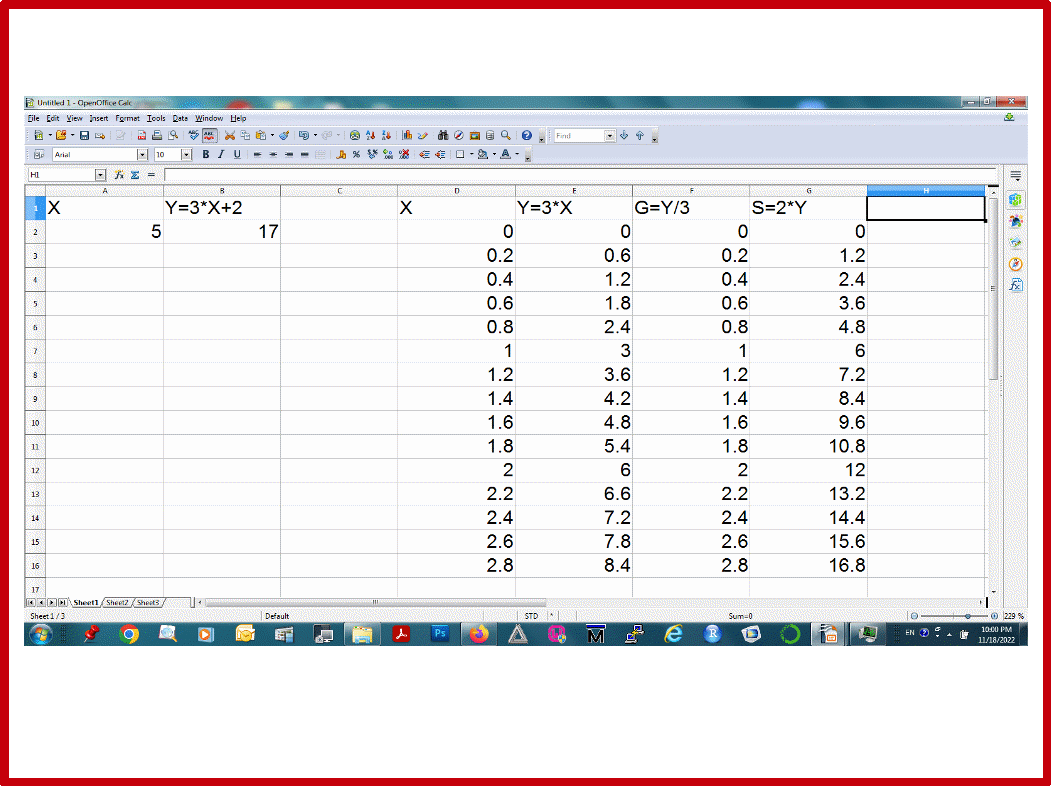
Рис.28.
Другая интересная особенность функции G, это то, что ее значения равны значениям исходного множества X, с которого все началось. Т.е. функция Y что-то сделала с числами X. А функция совершила действия обратные тому, что сделала функция Y, и все вернулось в исходное состояние. Говорят, что функция G является обратной функции Y.
Постройте графики функций Y от Х, G от Y, и G от X. Подсказка: если надо построить, например, G от Y, то в этом случае в областью определения функции G является Y. Поэтому в OpenOffice SpreadSheets, Range for X-values будут числа колонки Е, Range for X-values будут числа колонки F.
b) Аналогичным образом, найдите значения еще одной «функции от функции» S=2*Y (Рис.28) и постройте графики S от Y, Y от X, и S от X. Если бы вы записали функцию S от X аналитически, какое бы уравнение вы получили?
Задача 6.
Пусть множество Х будут числа от 0 до 24 с шагом 0.2 , и они будут в колонке А (Рис.29). Построим сначала таблицы функций Y=sin(X) и Z=cos(X). Пусть значения Y будут в колонке В, значения Z будут в колонке С (Рис.29). Надо построить графики функций Y от X , Z от X, и Z от Y.
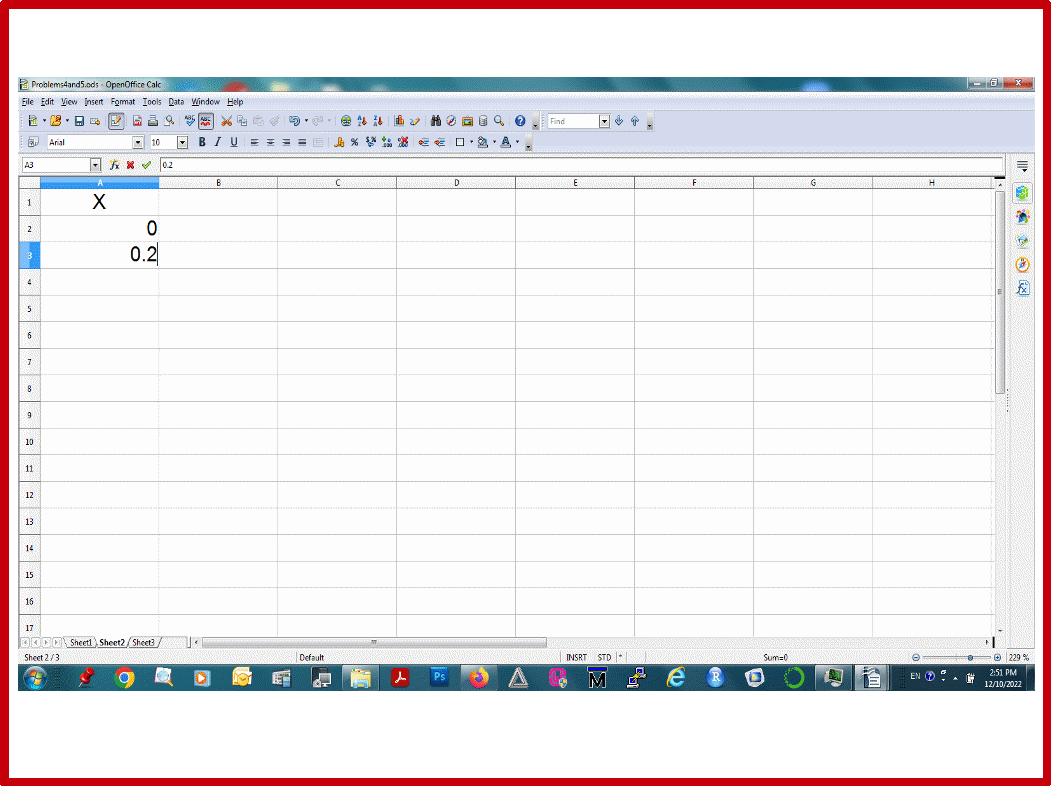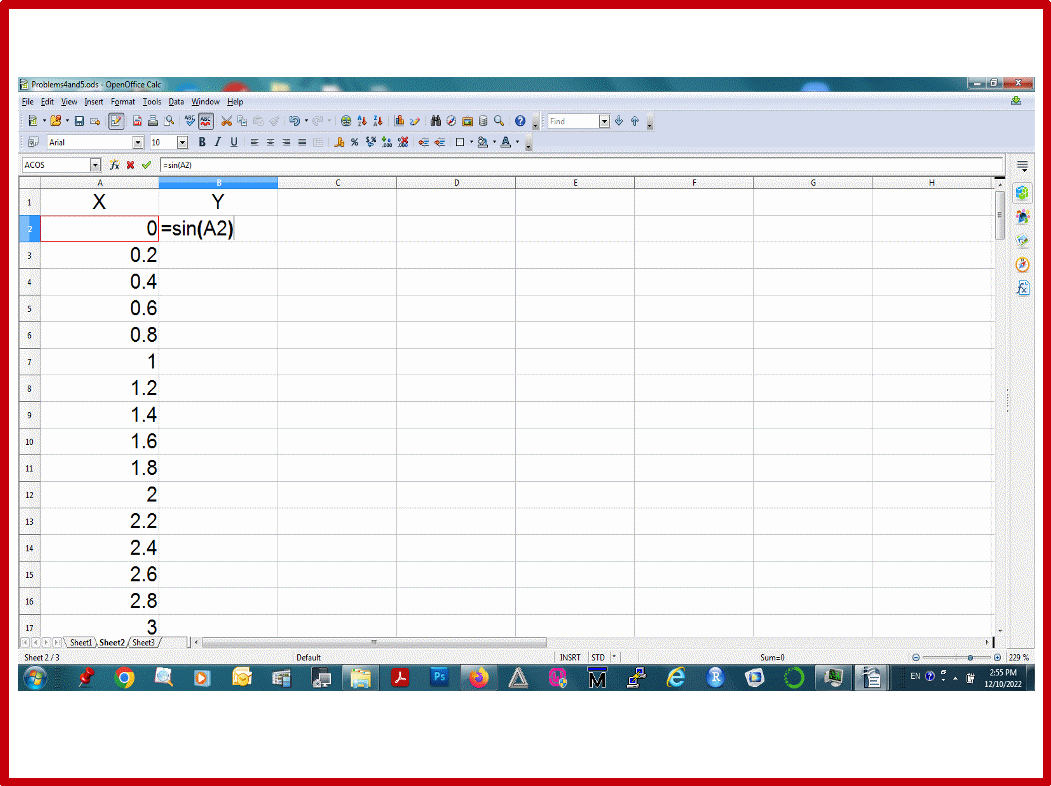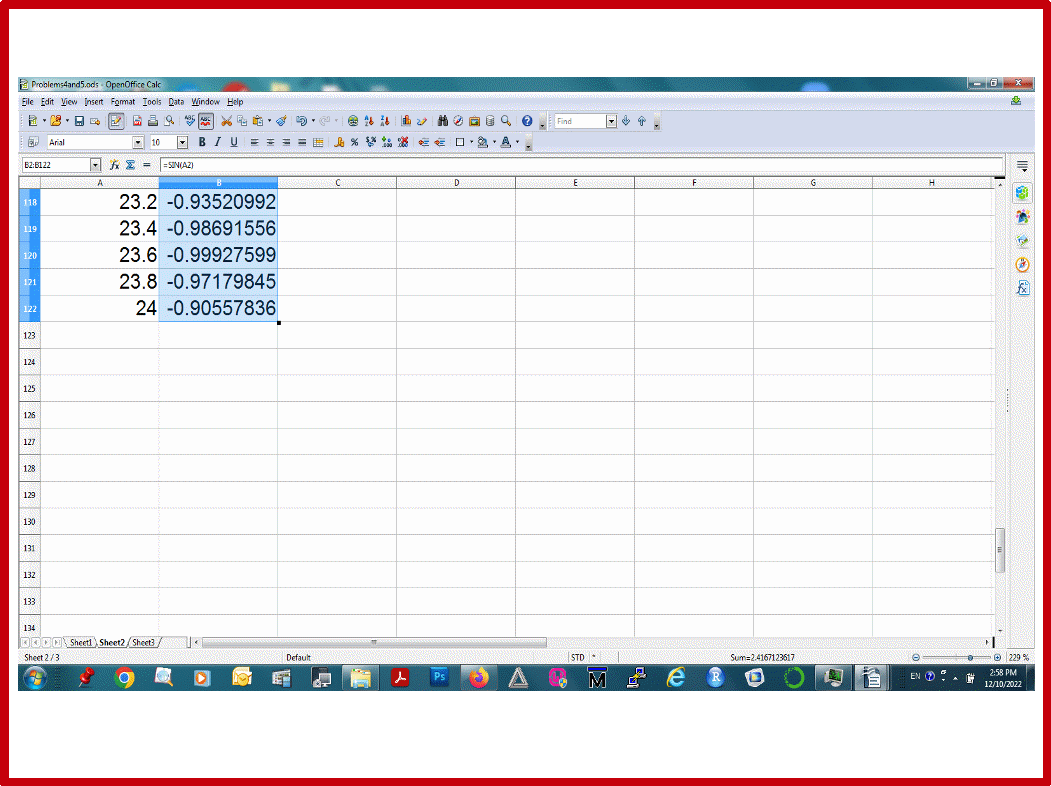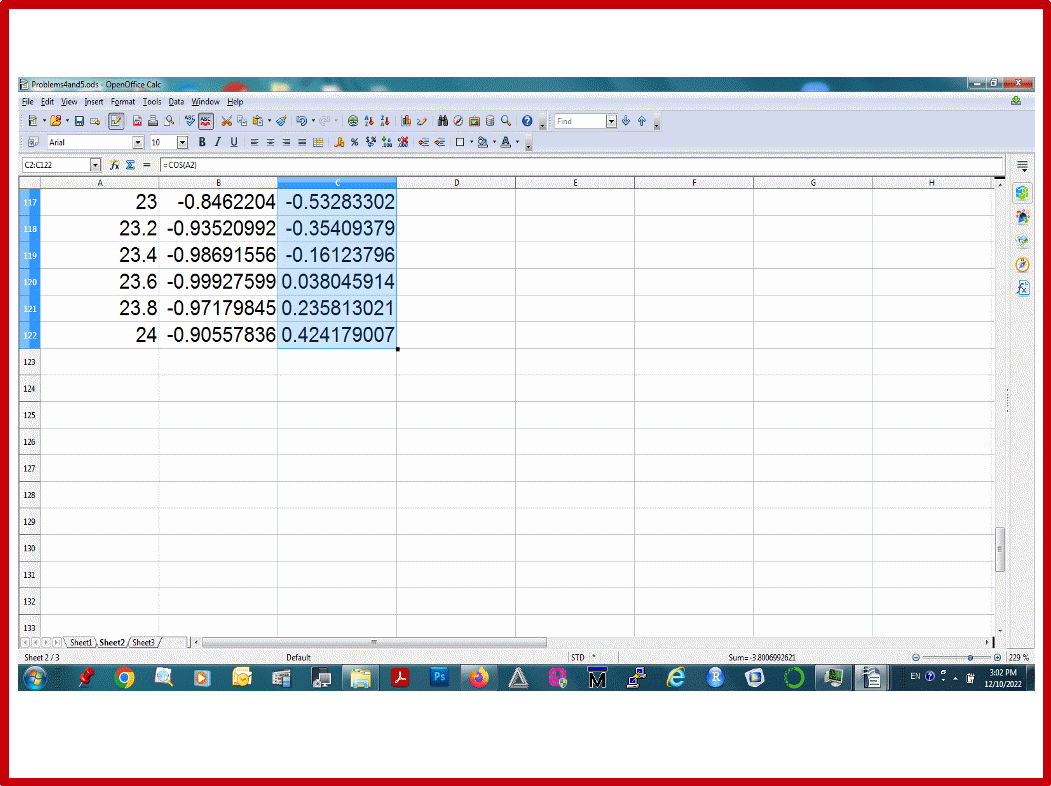
Рис.29.
Внимание!!: мы обозначаем колонки буквами X, Y, Z для нашего удобства. Компьютер этого не понимает. Он знает только, что первая колонка- это колонка А, вторая колонка- это колонка В, а третья колонка- это колонка С. Поэтому, в уравнениях для компьютера мы используем для колонок имена А, В, и С.
Например: в третьей строке колонки В, должно быть записана функция =sin(A3). Т.е. функция Y=sin(X), преобразует число ячейки A3 в число =sin(A3) ячейки В3. А во второй строке колонки С должно быть =cos(A2), что означает, что число ячейки А2 преобразуется в число cos(A2) ячейки С2.
Когда же мы строим графики, то все величины области определения функции, которые компьютер будет откладывать по горизонтальной оси, для него носят название X-values или Range for X-values. А все величины области значения функции, которые будут откладываться по вертикальной оси, компьютер называет Y-values или Range for Y-values. Но задавать эти области/множества/ranges мы должны опять с помощью компьютерных имен колонок А, В, С, D и так далее.
Задача 7.
В предыдущей Задаче 6, мы строили графики функций Y от X , Z от X, и Z от Y. Y получалась из X с помощью преобразования Y=sin(X). Z получалась из X с помощью функции Z=cos(X). Но мы еще построили график Z от Y, а значит построили функцию, которая преобразует Y в Z. Как же мы смогли осуществить это преобразование Y->Z, ведь мы не преобразовывали величины Y в величины Z ?
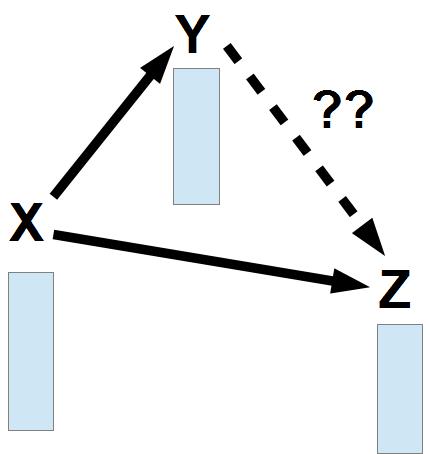
Объясните, как можно получить преобразование Y->Z с помощью
преобразований X->Y и X->Z (рис.30).
Или тоже самое можно сказать другими словами: Вы знаете, как попасть из X в Y: X->Y. Вы знаете, как попасть из X в Z: X->Z. А как попасть из Y в Z: Y->Z?
Попытайтесь найти два разных способа, как это сделать (подсказка: первый способ, через обратную функцию, а второй использует только одно «прямое» преобразование. Именно этот второй способ и был использован программой OpenOffice).
Задача 8.
Зададим теперь величины X, Y, Z, G, Q следующим образом. Величины Х запишем в колонку А. Пусть как и ранее, это будут числа от 0 до 24 с шагом 0.2.
Пусть Y опять задается преобразованием Y=sin(X). Результаты преобразований запишем в колонку В. В колонку С запишем результаты преобразования Z=cos(X). В колонку D занесем результаты преобразования G=2*cos(X). В колонку Е занесем результаты преобразования Q=2*cos(X+1). Постройте графики функций (все стройте на одном и том же графике для задачи 7):
1. Z от X
2. G от X
3. Q от X
4. Z от Y
5. G от Y
6. Q от Y
7. Q от G
Что у вас получилось?
Задача 9.
Запишем Х запишем в колонку А. Пусть это будут числа от -20 до 20 с шагом 1. Запишем теперь в колонки B, C, D, E переменные Y, Z, G, Q , где
Y= 2*X
Z= 2*X +5
G= 4*X
Q=2*(X+3)
Постройте графики функций (все стройте на одном и том же графике для задачи 8):
8. Y от X
9. G от X
10. Q от X
11. G от Y
Какие закономерности вы обнаружили?
Задача 10.
Вы уже много раз задавали область определения функций, например, с помощью чисел от 0 до 24 с шагом 0.2 (любой набор чисел в математике называется множеством чисел. А множество чисел, в котором каждому числу можно присвоить порядковый номер, называют числовым рядом. В нашем случае- это тоже числовой ряд). А что делать, если потребуется задать ряд чисел с шагом 0.1 или с шагом 2? Очевидно, придется перезаписывать весь столбец множества определения. Но можно поступить и иначе, изменив только одно число, равное шагу. Как это сделать?
Для этого нам потребуется рекуррентный способ задания функции. Рассмотрим пример такого способа задания числового ряда. На рисунке 31а приведены три первые строки колонок А и С. Запишем в ячейку С2 число равное шагу 0.1. В колонке А определим значение каждой ячейки через предыдущую. В первой ячейке ряда А2 запишем просто число 1 так, как для неё нет предыдущей ячейки. В ячейку А3 запишем функцию =A2 + C$2. Таким образом значение ячейки А3 станет равным значению ячейки А2 плюс значение ячейки С$2. Скопируем ячейку А3 вниз до ячейки А20 (Рис. 31б). Обратите внимание адреса ячеек колонки А записываются без знака доллара, а адрес ячейки С$2 со знаком доллара перед цифрой, координатой строки. Таким образом мы фиксируем при копировании адресацию к ячейке С$2 из любых ячеек колонки А. Ещё можно было бы записать этот адрес как $С$2. Тогда мы бы зафиксировали при копировании адресацию к этой ячейки из любой ячейки таблицы.
Вы задали рекуррентным способом числовой ряд колонки А. Поменяйте значение шага в ячейке С2 (например, запишите туда число 1 или 2), и посмотрите, что стало с множеством чисел колонки А.
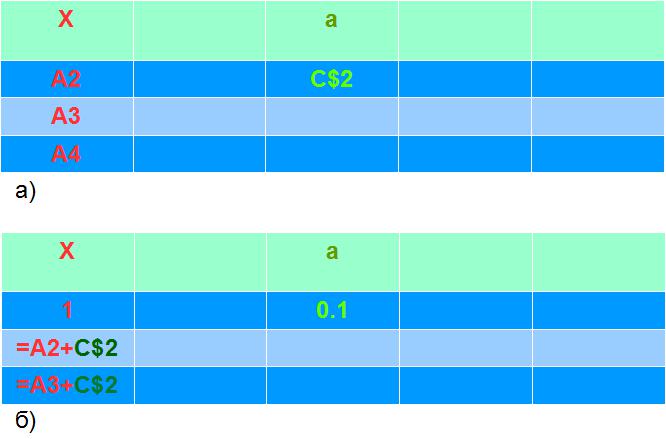
Рис.31
Задайте теперь множество чисел колонки В с помощью функции Y=2*X, как показано на рисунке 32. Для этого сначала, как обычно, запишите в ячейку В2 функцию=2*A2. Затем, скопируйте значение ячейки на все остальные, до ячейки В20. Постройте график Yот Х. Посмотрите, как меняется график если вы будете менять значение шага в ячейке С2. Чтобы были лучше видны изменения, зафиксируйте максимальное и минимальное значение по осям, как это сделано в учебном видео https://youtu.be/YqrAwxJkRIA . Величины X и Y, которые используют для обозначения множеств определения и значения, называются переменными. Величина а называется параметром данной функции.
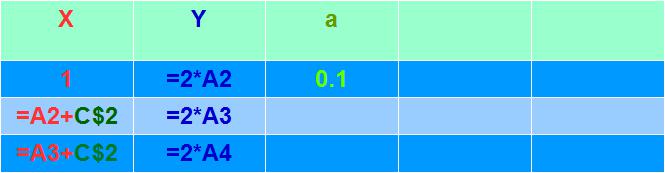
Рис.32.
Для определения множества Y, мы использовали функцию Y=2*X. Но часто будут возникать ситуации, когда потребуется рассмотреть и другие преобразования. Например, Y=3*X или Y=10*X. Чтобы упростить работу, здесь можно использовать еще один параметр, назовем его b. Запишем его значение в ячейку D2 (Рис.33) и запишем значения множества Y, в виде Y=b*X.
Для этого в ячейку В2 запишем =D$2*A2, и затем скопируем её до ячейки D20.
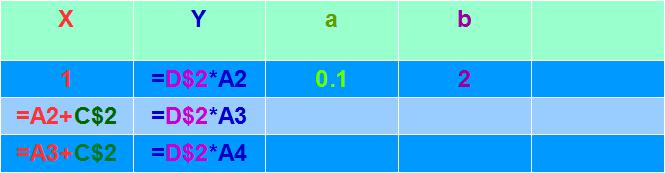
Рис.33.
Постройте график получившейся функции Y от X. Посмотрите, как меняется график при изменении величин b и a.
Задача 11.
В задаче 10 вы построили график функции Y=b*X, где b -параметер. Теперь, аналогичным образом, сами постройте график функции Y=b*X + c, где b и c параметры. Используйте такую же область определения Х, как и в задаче 10. Посмотрите, как меняется график при изменении величин c, b и a.
Задача 12.
Рассмотрим применение полученных знаний к конкретной физической задаче. Видео https://www.youtube.com/watch?v=D8EeqbV6-Xw&feature=youtu.be показывает, как движется тележка, которую тянет за собой падающий груз. На рисунке 34 схематично показано движение одной из тележек представленных на видео. Рисунок объясняет, как измеряется пройденный путь, скорость и ускорение тележки с грузом в этом случае. Используя полученную на рисунке таблицу, создайте аналогичную таблицу в OpenOffice для величин t, L, v, и a (можно сохранить горизонтальную таблицу, как на рисунке, но удобнее сделать таблицу вертикальной, как мы делали ранее). Здесь t означает время движения тележки, измеренное в секундах, L-пройденный тележкой путь измеренный в миллиметрах, v -скорость тележки измеренная в мм/сек и a-усорение тележки в мм/(сек*сек). Постройте графики L от t, v от t, a от t. Какие закономерности движения тележки видны из этих графиков? Смогли бы вы обнаружить эти закономерности без графиков?
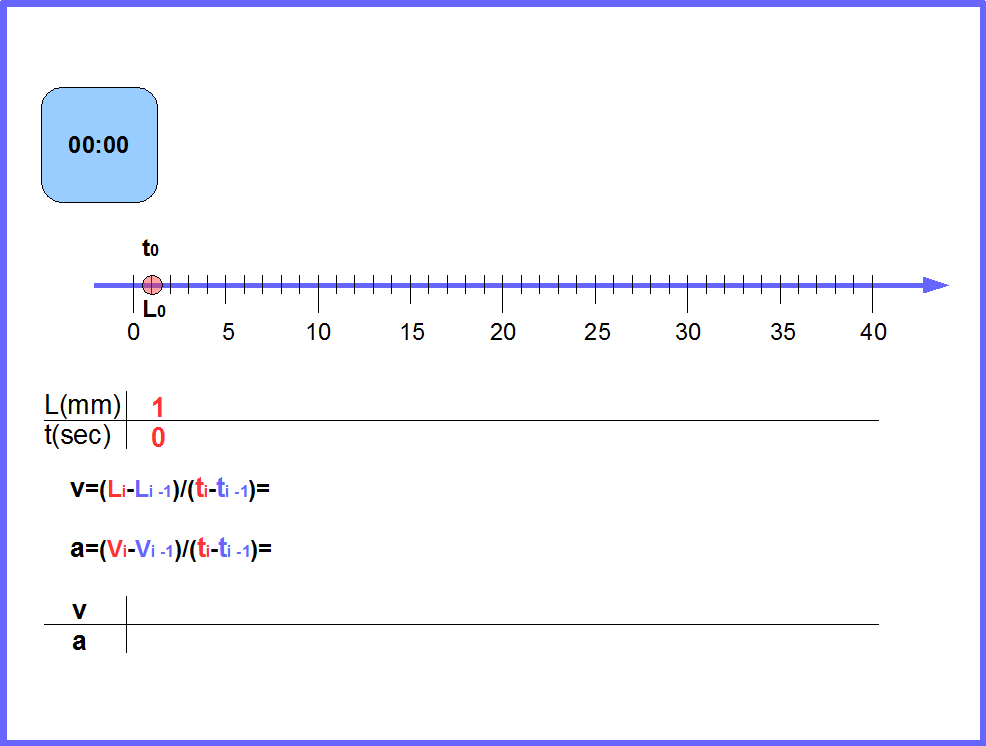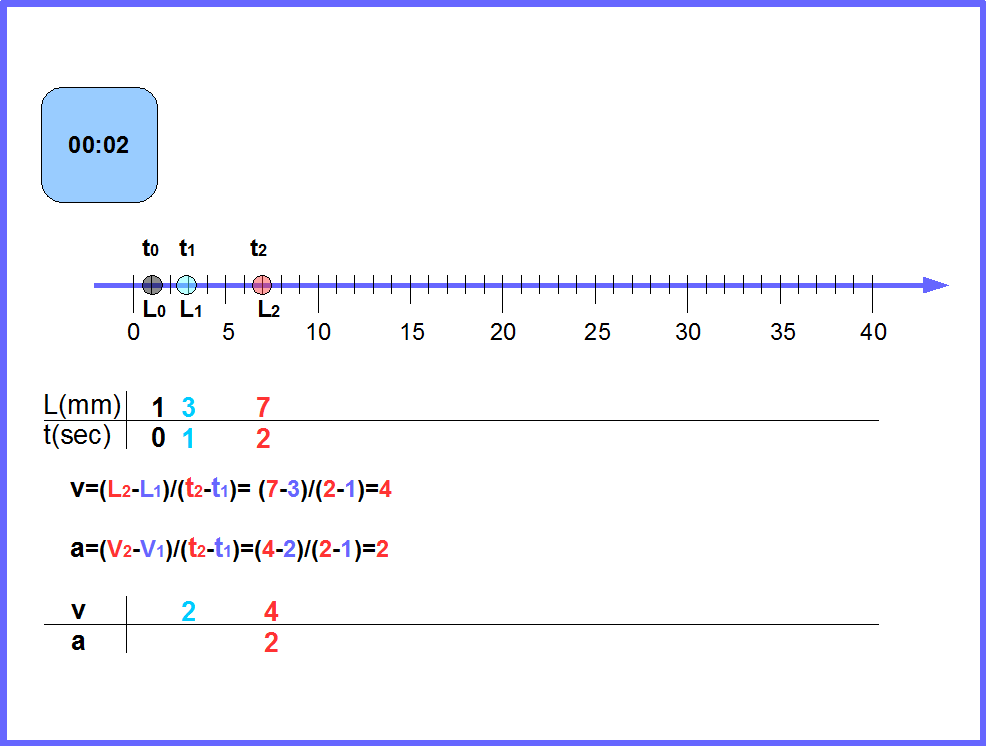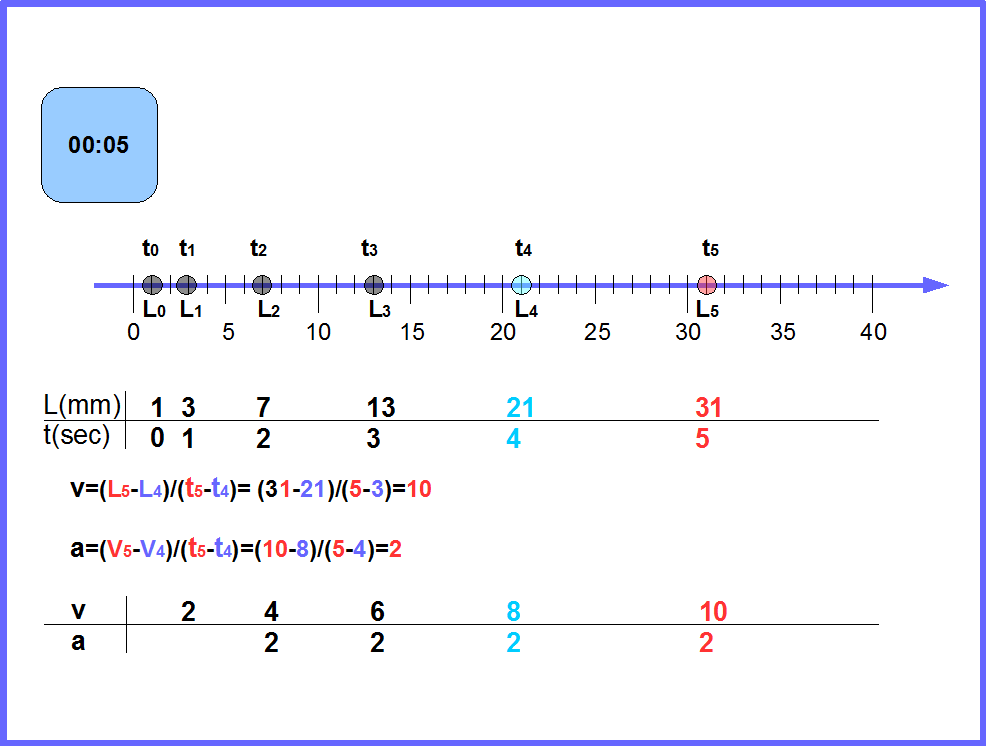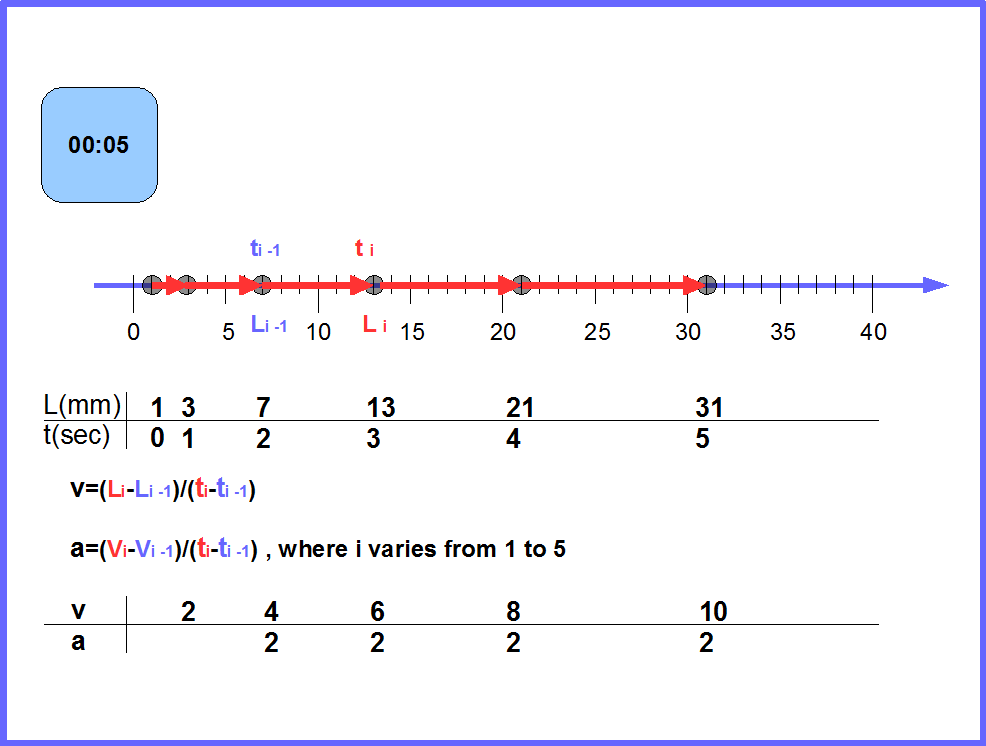
Рис.34